TACTiS: Transformer-Attentional Copulas for Time Series (2202.03528v2)

Abstract: The estimation of time-varying quantities is a fundamental component of decision making in fields such as healthcare and finance. However, the practical utility of such estimates is limited by how accurately they quantify predictive uncertainty. In this work, we address the problem of estimating the joint predictive distribution of high-dimensional multivariate time series. We propose a versatile method, based on the transformer architecture, that estimates joint distributions using an attention-based decoder that provably learns to mimic the properties of non-parametric copulas. The resulting model has several desirable properties: it can scale to hundreds of time series, supports both forecasting and interpolation, can handle unaligned and non-uniformly sampled data, and can seamlessly adapt to missing data during training. We demonstrate these properties empirically and show that our model produces state-of-the-art predictions on multiple real-world datasets.

• The paper introduces tact, a transformer-based approach that leverages attentional copulas for accurate multivariate time series prediction.
• It integrates an encoder for observed and missing tokens with a decoder using neural networks and normalizing flows for density estimation.
• Empirical studies show tact’s superior performance in forecasting, interpolation, and handling irregularly sampled data across multiple datasets.

Transformer-Attentional Copulas for Time Series: A Deep Dive

This essay provides a comprehensive review of the paper "TACTiS: Transformer-Attentional Copulas for Time Series" (2202.03528), which introduces a novel approach, termed tact, for estimating the joint predictive distribution of high-dimensional multivariate time series. tact leverages the transformer architecture and introduces attentional copulas, enabling versatile time series analysis, including forecasting, interpolation, and handling irregularly sampled data.

Core Contributions of TACTiS

The paper makes several significant contributions to the field of time series analysis. First, it presents tact, a flexible transformer-based model designed for large-scale multivariate probabilistic time series prediction. A key innovation is the introduction of attentional copulas, an attention-based architecture capable of estimating non-parametric copulas for an arbitrary number of random variables. The authors provide a theoretical proof of the convergence of attentional copulas to valid copulas. Finally, an empirical paper demonstrates tact's state-of-the-art probabilistic prediction accuracy on multiple real-world datasets, highlighting its flexibility.

Model Architecture and Implementation

tact's architecture comprises an encoder and a decoder. The encoder, similar to standard transformers, encodes both observed and missing tokens. The decoder, based on an attentional copula, learns the output density given representations of the observed and missing tokens (Figure 1).

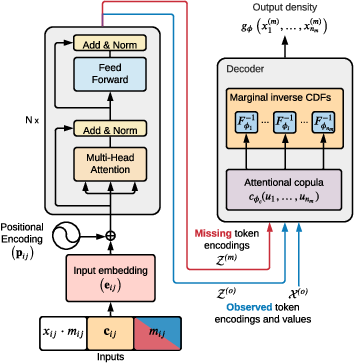
Figure 1: Model overview. (Left) The tact encoder is very similar to that of standard transformers. The key difference is that both observed and missing tokens are encoded simultaneously. (Right) The decoder, based on an attentional copula, learns the output density given representations of the observed and missing tokens.

The encoder starts by producing a vector embedding for each element in each time series, accounting for its value, associated covariates, and whether it is observed or missing. Positional encoding, based on sine and cosine functions, adds information about a token's timestamp to the input embedding. The embeddings are then passed through a stack of residual layers that combine multi-head self-attention and layer normalization to obtain an encoding for each token.

The decoder estimates the joint density of missing token values using an attention-based architecture trained to mimic a non-parametric copula. The model uses normalizing flows to model the marginal CDFs. The parameters of each flow are produced by a neural network. An overview of the tact decoder architecture is shown in (Figure 2).

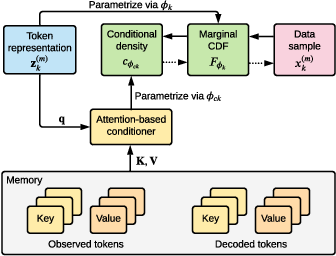
Figure 2: Overview of the tact decoder architecture. Dotted arrows indicate the flow of information during sampling.

The copula density is factorized autoregressively, and an attention-based conditioner produces the parameters for the conditional density. Any distribution with support on $[0, 1]$ can be used to model the conditional distributions. The authors chose to use a piecewise constant distribution.

Theoretical Foundation

The paper provides a theoretical guarantee that the attentional copula embedded in the density estimator is a valid copula. This guarantee relies on the fact that the training procedure, which minimizes the expected negative log-likelihood of the model over permutations drawn uniformly at random, leads to permutation invariance and, consequently, to uniform marginal distributions.

Empirical Validation and Results

The authors conducted several experiments to validate the proposed approach. First, they empirically validated attentional copulas by demonstrating that the learned copula density closely matches the ground truth density (Figure 3a), and its marginal distributions are indistinguishable from the $U_{[0, 1]}$ distribution (Figure 3b).

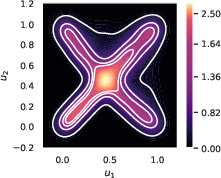
Figure 3: Attentional copulas successfully learn valid copulas. a) The learned copula's density (white contours) closely matches the ground truth (heatmap). Note: the support of both distributions is [0, 1]; any visible overflow in the figure is due to plotting artefacts. b) The marginal distributions of the learned copula are indistinguishable from $U_{[0, 1]}$.

The performance of tact was assessed by comparison with state-of-the-art forecasting methods on five real-world datasets. The results, measured using the CRPS-Sum, show that tact compares favorably to existing methods, achieving the lowest CRPS-Sum for three out of five datasets.

The flexibility of the tact model was demonstrated through experiments involving interpolation, unaligned and non-uniformly sampled data, and scalability to hundreds of time series. For instance, tact accurately estimates the distribution of a gap in observed values within a stochastic volatility process (Figure 4).

Figure 4: tact successfully interpolates missing values (green shaded region) within a stochastic volatility process. The estimated posterior distribution of missing values (top) closely matches the ground truth (bottom).

tact also supports unaligned and non-uniformly sampled time series, as demonstrated by forecasts of a bivariate noisy sine process (Figure 5).

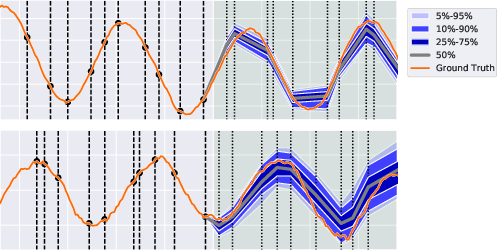
Figure 5: tact supports unaligned and non-uniformly sampled time series, as shown in the above forecasts of a bivariate noisy sine process. Observation and prediction timestamps are marked by dashed vertical lines. The forecasted portion of the time series is shaded in green.

Backtesting and Evaluation

The paper utilizes a rigorous backtesting procedure to mimic real-world forecasting scenarios (Figure 6). The model accuracy is assessed using the CRPS-Sum and other metrics. The authors report that tact achieves state-of-the-art performance on several real-world datasets.

Figure 6: A visual representation of how the data is split during hyperparameter search and backtesting with n_B = 2 and n_F = 3. During backtesting, the models are trained at times tau_i, and are used for forecasting at times $\tau_{ij}$.

Limitations and Future Directions

Despite its strengths, tact has certain limitations. The computational complexity of self-attention, scaling quadratically with the number of tokens, poses a challenge. The authors suggest that future research could focus on improving the efficiency of transformers and exploring positional encodings tailored to time series data. Extending tact to series measured in discrete domains and addressing the cold-start problem are also promising directions for future work.

Conclusions

tact represents a significant advancement in probabilistic time series inference. By combining the flexibility of attention-based models with the density estimation capabilities of attentional copulas, tact achieves state-of-the-art performance on a variety of tasks. The model's ability to handle missing data, unaligned time series, and complex distributions makes it a valuable tool for researchers and practitioners in various domains.