Math Word Problem Generation with Mathematical Consistency and Problem Context Constraints (2109.04546v1)

Abstract: We study the problem of generating arithmetic math word problems (MWPs) given a math equation that specifies the mathematical computation and a context that specifies the problem scenario. Existing approaches are prone to generating MWPs that are either mathematically invalid or have unsatisfactory language quality. They also either ignore the context or require manual specification of a problem template, which compromises the diversity of the generated MWPs. In this paper, we develop a novel MWP generation approach that leverages i) pre-trained LLMs and a context keyword selection model to improve the language quality of the generated MWPs and ii) an equation consistency constraint for math equations to improve the mathematical validity of the generated MWPs. Extensive quantitative and qualitative experiments on three real-world MWP datasets demonstrate the superior performance of our approach compared to various baselines.

• The paper introduces a conditional generation framework using GPT-2 to produce math word problems that are both mathematically consistent and contextually relevant.
• It integrates an equation consistency constraint and a context keyword selection model, enhancing generation diversity and validity compared to traditional seq2seq models.
• Experimental results on Arithmetic, MAWPS, and Math23K datasets demonstrate significant improvements in language quality metrics and equation accuracy.

Math Word Problem Generation with Mathematical Consistency and Problem Context Constraints

Introduction

The paper addresses the problem of generating math word problems (MWPs) from given mathematical equations and contexts. Traditional approaches in MWP generation face challenges in generating problems that are both mathematically consistent and contextually relevant. The proposed methodology leverages pre-trained LLMs to enhance language quality while incorporating an equation consistency constraint alongside a context keyword selection model. These components aim to achieve high-quality language outputs that are consistent with the given equation and context.

Methodology

The methodology employs a conditional generation framework involving a pre-trained LLM (LM). The goal is to generate mathematically valid and contextually coherent MWPs given input equations and contexts:

1. LLM Framework: A GPT-2 model is used as the generative backbone. The input comprises an equation and context, generating an MWP ensuring language consistency.
2. Equation Consistency Constraint: Introduced to ensure mathematical validity by parsing generated MWPs back into equations and aligning them with the input using an mwp2eq model.
3. Context Selection Model: Employs a learned context keyword selection model, codifying contexts into a bag-of-keywords format extracted from MWPs.

The generative process is formalized as a conditional LLM focusing on both language quality and mathematical consistency, enhanced by employing Gumbel-softmax distribution for differentiable sampling processes.

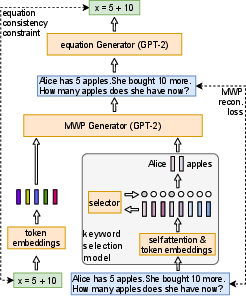
Figure 1: An illustration of our MWP generation approach and its key components.

Experimental Results

The approach was validated on three datasets: Arithmetic, MAWPS, and Math23K, showing superior performance against sequence-to-sequence baselines. The metrics used were BLEU-4, METEOR, ROUGE-L for language quality, and equation accuracy for mathematical validity. The results demonstrated notable improvements in generating MWPs with high language quality and mathematical consistency:

• LLMs pre-trained and fine-tuned on targeted data exceeded seq2seq baselines in most quality metrics.
• Ablations confirmed the importance of both the equation consistency constraint and context keyword selection in enhancing generation consistency and diversity.

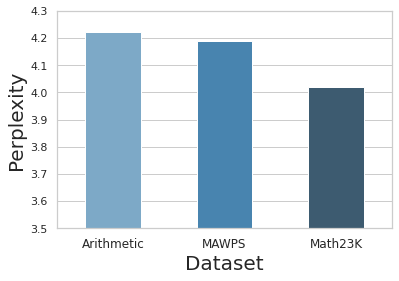
  Figure 2: Averaged perplexity of each dataset under a small GPT-2. The translated Math23K dataset has similar perplexity compared to the other two datasets, suggesting similar language quality of the three datasets.

  

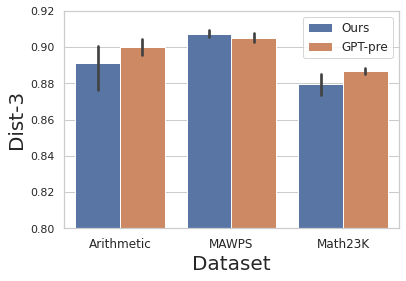
  Figure 3: Diversity of generation comparing our approach with a fine-tuned pre-trained GPT-2. Our approach achieves similar generation diversity according to the Dist-3 metric.

Limitations

While the approach showed improvements, several issues were highlighted. Common errors include incomplete information, incorrectly posed questions, and semantically incoherent statements. These errors suggest areas for future enhancement, particularly in better understanding the semantics of mathematical operations and improving the coherence between mathematical and linguistic components.

Conclusion

The paper presents an effective methodology for generating MWPs by integrating pre-trained LLMs with mathematical and contextual constraints. Despite successes, future work should focus on better handling complex, multi-variable equations and exploring advanced evaluation metrics for mathematical validity. Further exploration into improving model comprehension of mathematical semantics remains an area ripe for exploration.

The research's potential impact extends to educational technology, providing automated tools for educators in creating rich, mathematically consistent educational resources while offering personalized learning experiences.