AI Descartes: Combining Data and Theory for Derivable Scientific Discovery (2109.01634v4)

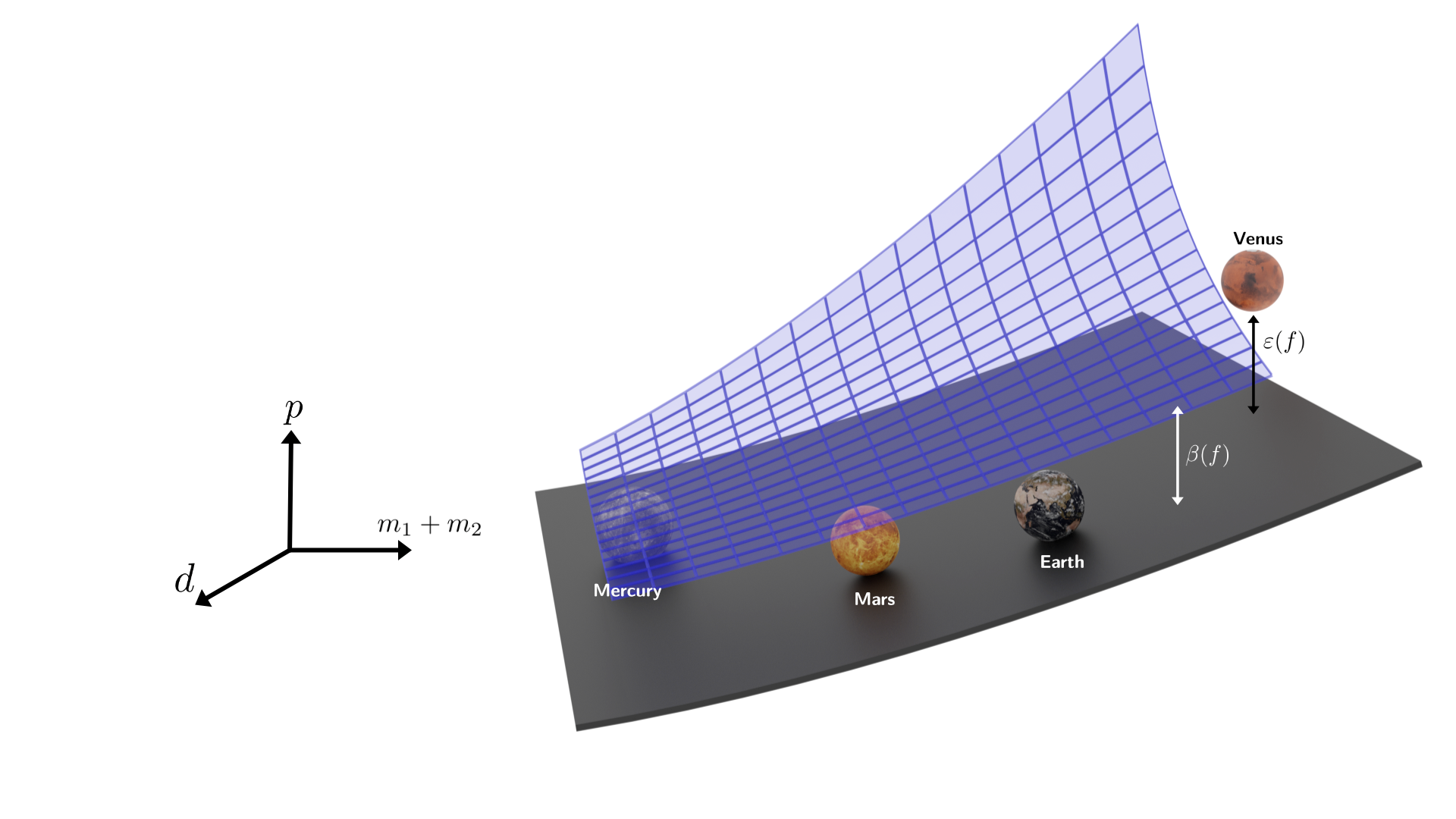
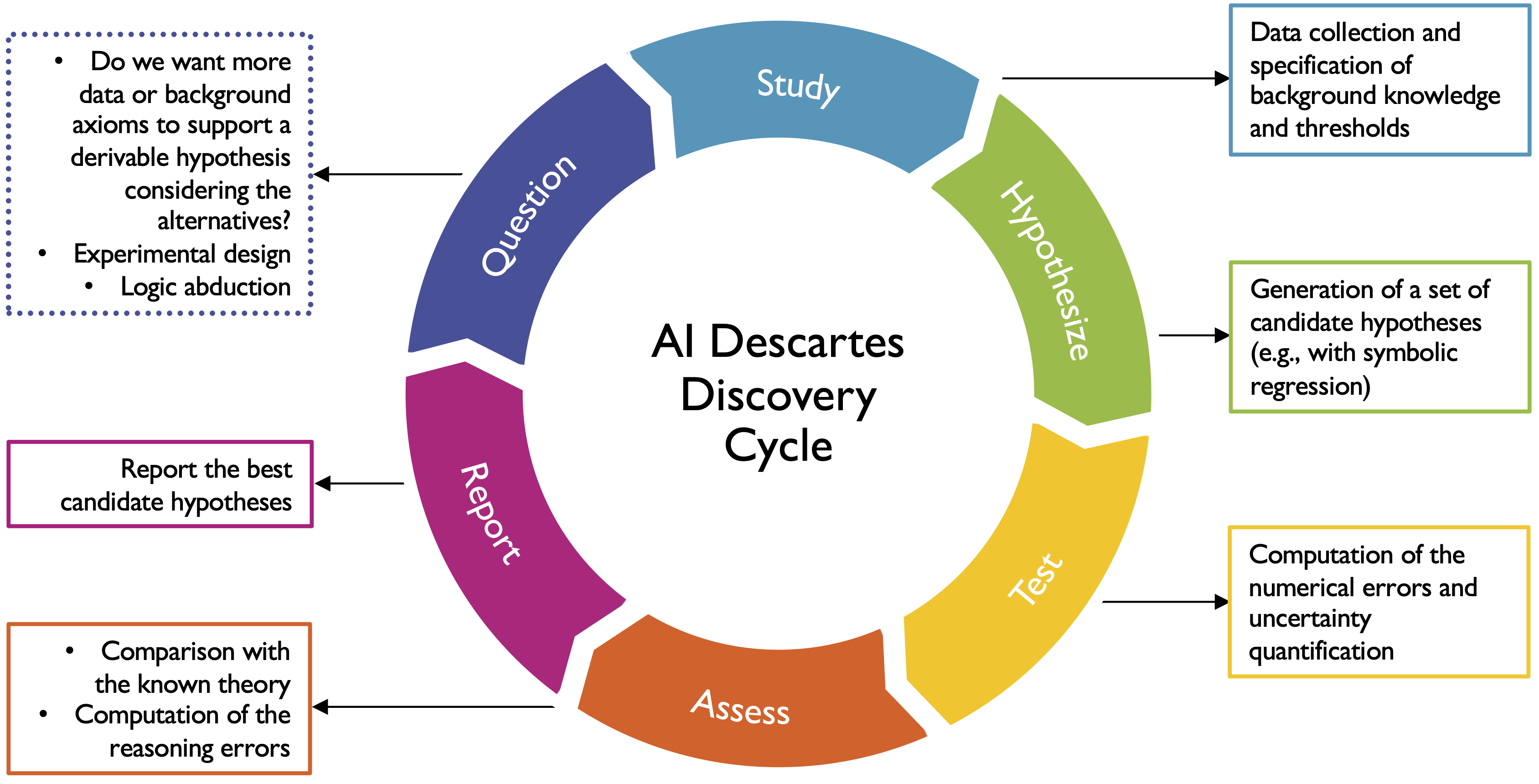
Abstract: Scientists have long aimed to discover meaningful formulae which accurately describe experimental data. A common approach is to manually create mathematical models of natural phenomena using domain knowledge, and then fit these models to data. In contrast, machine-learning algorithms automate the construction of accurate data-driven models while consuming large amounts of data. The problem of incorporating prior knowledge in the form of constraints on the functional form of a learned model (e.g., nonnegativity) has been explored in the literature. However, finding models that are consistent with prior knowledge expressed in the form of general logical axioms (e.g., conservation of energy) is an open problem. We develop a method to enable principled derivations of models of natural phenomena from axiomatic knowledge and experimental data by combining logical reasoning with symbolic regression. We demonstrate these concepts for Kepler's third law of planetary motion, Einstein's relativistic time-dilation law, and Langmuir's theory of adsorption, automatically connecting experimental data with background theory in each case. We show that laws can be discovered from few data points when using formal logical reasoning to distinguish the correct formula from a set of plausible formulas that have similar error on the data. The combination of reasoning with machine learning provides generalizeable insights into key aspects of natural phenomena. We envision that this combination will enable derivable discovery of fundamental laws of science and believe that our work is an important step towards automating the scientific method.

AI Descartes: Combining Data and Theory for Derivable Scientific Discovery

Overview

The paper "AI Descartes: Combining Data and Theory for Derivable Scientific Discovery" explores a novel technique for scientific model discovery by integrating symbolic regression with logical reasoning. The approach aims to automate the derivation of scientific laws from experimental data and background theoretical knowledge. This method leverages symbolic regression to hypothesize potential models, which are then evaluated and verified for consistency with known scientific axioms using logical reasoning.

Methodology

The proposed system operates on four key components: background knowledge, hypothesis class, experimental data, and modeler preferences. Background knowledge consists of prior axioms defining the domain, while the hypothesis class specifies the functional form of symbolic models. The symbolic regression module generates candidate expressions, represented as trees of mathematical operations. After generating hypotheses, a logical reasoning system evaluates the provability of these expressions from the axioms provided in the background knowledge.

Figure 1: Depiction of the numerical data, background theory, and a discovered model for Kepler’s third law.

Symbolic Regression and Logical Reasoning

Symbolic regression attempts to discover equations that fit experimental data without predetermined functional forms. In order to produce scientifically interpretable models, the approach combines mathematical optimization techniques with symbolic regression. This phase generates multiple model hypotheses that are ranked based on fit and complexity. The logical reasoning component then determines whether these models can be derived from established scientific laws, refining the hypothesis space.

Figure 2: System overview illustrating the integration of symbolic regression and logical reasoning.

Applications

The efficacy of the AI Descartes system is demonstrated through various scientific laws including Kepler's third law, Einstein’s time dilation, and Langmuir's adsorption theory. For each case, the system successfully connected experimental data with corresponding scientific background theory, enabling the reconstruction of known laws with fewer data points. This integration allows the derivation of accurate and theoretically sound scientific models, emphasizing the potential for automating scientific discovery processes.

Results

AI Descartes shows promising results in rediscovering known scientific