Efficient Stepping Algorithms and Implementations for Parallel Shortest Paths (2105.06145v3)

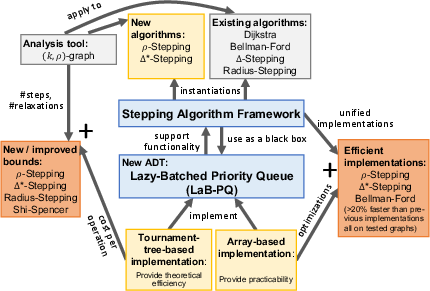
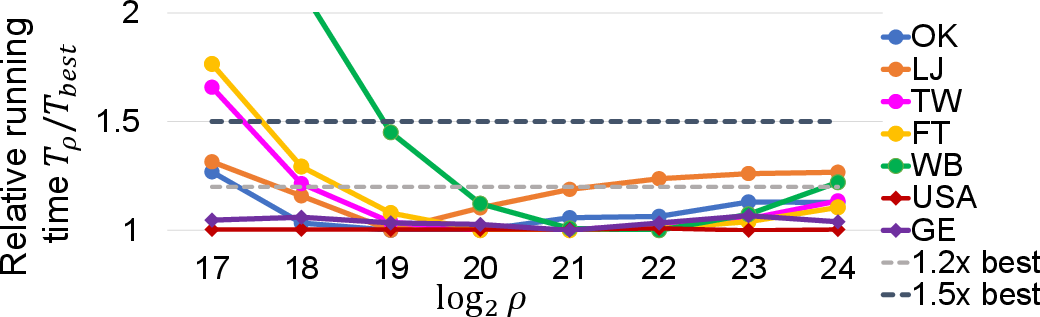
Abstract: In this paper, we study the single-source shortest-path (SSSP) problem with positive edge weights, which is a notoriously hard problem in the parallel context. In practice, the $\Delta$-stepping algorithm proposed by Meyer and Sanders has been widely adopted. However, $\Delta$-stepping has no known worst-case bounds for general graphs. The performance of $\Delta$-stepping also highly relies on the parameter $\Delta$. There have also been lots of algorithms with theoretical bounds, such as Radius-stepping, but they either have no implementations available or are much slower than $\Delta$-stepping in practice. We propose a stepping algorithm framework that generalizes existing algorithms such as $\Delta$-stepping and Radius-stepping. The framework allows for similar analysis and implementations of all stepping algorithms. We also propose a new ADT, lazy-batched priority queue (LaB-PQ), that abstracts the semantics of the priority queue needed by the stepping algorithms. We provide two data structures for LaB-PQ, focusing on theoretical and practical efficiency, respectively. Based on the new framework and LaB-PQ, we show two new stepping algorithms, $\rho$-stepping and $\Delta^*$-stepping, that are simple, with non-trivial worst-case bounds, and fast in practice. The stepping algorithm framework also provides almost identical implementations for three algorithms: BeLLMan-Ford, $\Delta^*$-stepping, and $\rho$-stepping. We compare our code with four state-of-the-art implementations. On five social and web graphs, $\rho$-stepping is 1.3--2.5x faster than all the existing implementations. On two road graphs, our $\Delta^*$-stepping is at least 14\% faster than existing implementations, while $\rho$-stepping is also competitive. The almost identical implementations for stepping algorithms also allow for in-depth analyses and comparisons among the stepping algorithms in practice.

• The paper introduces a stepping algorithm framework using LaB-PQ to optimize parallel SSSP, generalizing the popular Δ-stepping method.
• It features new algorithms ρ-stepping and Δ*-stepping that achieve up to 2.6x speedup on social, web, and road graphs with improved theoretical bounds.
• The study emphasizes lazy batching and efficient data structures, offering practical scalability on multi-core systems with complex memory hierarchies.

Efficient Stepping Algorithms and Implementations for Parallel Shortest Paths

Introduction

The paper "Efficient Stepping Algorithms and Implementations for Parallel Shortest Paths" presents a framework and new algorithms to tackle the SSSP problem in a parallel computing context. It extends the use of the $\Delta$-stepping algorithm, popular due to its practical efficiency, by offering a stepping algorithm framework that generalizes many existing algorithms while also introducing a novel abstract data type (ADT), LaB-PQ, that facilitates more efficient priority queue operations.

Stepping Algorithm Framework

The proposed framework abstracts the conventional stepping algorithms through the integration of the stepping procedure shared by $\Delta$-stepping and other similar algorithms. In this framework:

• ExtDist is a function that determines which vertices should be processed in a given step.
• FinishCheck determines whether additional processing is necessary within the current step.

By employing the LaB-PQ ADT, this framework efficiently manages vertex processing by relaxing vertices' neighbors whose distances are minimal within a determined threshold. This priority queue is designed to handle updates lazily and in batches for efficiency.

Figure 1: An overview of all components in this paper and how they are put together.

Algorithmic Contributions

• $\rho$-stepping and $\Delta^*$-stepping Algorithms: Two new algorithms are introduced. $\rho$-stepping emphasizes relaxing a fixed number of vertices in each step, offering both practical and theoretical performance advantages. $\Delta^*$-stepping, a variant of the traditional $\Delta$-stepping, shows improved bounds by effectively removing the complexity tied to selecting $\Delta$.
• Performance and Theoretical Improvements: $\rho$-stepping is 1.3-2.6x faster than existing implementations across social and web graphs and shows competitive results in road networks. Moreover, $\Delta^*$-stepping is claimed to achieve at least a 14% improvement in road graphs over existing counterparts.

LaB-PQ: Optimization through Abstract Data Structures

The LaB-PQ is central to the stepping algorithms' optimization, focusing on:

• Lazy Batching: Priority queue updates are batched, allowing for efficient bulk processing.
• Efficient Data Structures: The authors introduce efficient implementations of LaB-PQ using competitive data structures like tournament trees and arrays, tailored for theoretical efficiency and practical performance.

  Figure 2: A tournament tree. Square leaf nodes store the records and round interior nodes keep the smallest key in their subtrees.

Performance Analysis and Results

• Work-Span Model: The paper uses the work-span model to evaluate parallel algorithms, considering both the total number of operations (work) and the longest sequence of dependent operations (span).
• Empirical Results: Extensive testing across several graph types demonstrates the significance of selecting the right $\rho$ for $\rho$-stepping, showing consistent performance across various real-world datasets, contrasting the sensitivities seen with $\Delta$ selection in $\Delta$-stepping.

  Figure 3: \smallRelative running time of with varied $\rho$. \mdseries We use 96 cores (192 hyperthreads).

Practical Implications and Future Directions

This research offers practical advancements in parallel computing for graph algorithms:

• Scalability: By optimizing at the level of both data structure and algorithm design, implementations are robust across architectures, particularly multi-core systems with complex memory hierarchies.
• Parameter Tuning: Future work might continue to explore adaptive mechanisms to automate parameter selection, particularly for $\rho$, potentially leveraging graph analytics to dynamically adjust parameters based on observed execution patterns.

Conclusion

The paper effectively bridges the gap between theoretical guarantees and practical performance for parallel SSSP. Its innovations in algorithmic design and data structure efficiency hold considerable promise for improving SSSP implementations, with broader implications for parallel algorithm design in computational graph theory.