Using latent space regression to analyze and leverage compositionality in GANs (2103.10426v2)

Abstract: In recent years, Generative Adversarial Networks have become ubiquitous in both research and public perception, but how GANs convert an unstructured latent code to a high quality output is still an open question. In this work, we investigate regression into the latent space as a probe to understand the compositional properties of GANs. We find that combining the regressor and a pretrained generator provides a strong image prior, allowing us to create composite images from a collage of random image parts at inference time while maintaining global consistency. To compare compositional properties across different generators, we measure the trade-offs between reconstruction of the unrealistic input and image quality of the regenerated samples. We find that the regression approach enables more localized editing of individual image parts compared to direct editing in the latent space, and we conduct experiments to quantify this independence effect. Our method is agnostic to the semantics of edits, and does not require labels or predefined concepts during training. Beyond image composition, our method extends to a number of related applications, such as image inpainting or example-based image editing, which we demonstrate on several GANs and datasets, and because it uses only a single forward pass, it can operate in real-time. Code is available on our project page: https://chail.github.io/latent-composition/.

• The paper introduces a latent space regression method that deciphers compositionality in GANs and enables diverse image manipulation tasks through a masking mechanism.
• It integrates a fixed pretrained generator with a regressor network to accurately recover latent codes, ensuring high-fidelity and coherent image reconstructions.
• Experimental results demonstrate that this approach outperforms traditional autoencoder and optimization techniques in both reconstruction realism and computational efficiency.

Investigating Compositionality in GANs Through Latent Space Regression

Introduction

Generative Adversarial Networks (GANs) have made significant strides in generating high-quality images from random noise, yet the underlying mechanisms by which GANs transform latent codes into visually coherent outputs remain elusive. This paper introduces a method using latent space regression to analyze and leverage the compositional properties of GANs. By combining a regressor network with a fixed, pretrained generator, the authors propose a framework to explore how image parts and properties are composed at the latent level.

Figure 1: Simple latent regression on a fixed, pretrained generator can perform a number of image manipulation tasks based on single examples without requiring labelled concepts during training. We use this to probe the ability of GANs to compose scenes from image parts, suggesting that a compositional representation of objects and their properties exists already at the latent level.

Methodology

Latent Code Recovery

The key method revolves around a regressor network trained to predict latent codes from input images. This is coupled with a fixed GAN generator, allowing the regression model to map input images onto the generated image manifold, subsequently achieving realistic image synthesis. The loss function used includes image reconstruction and perceptual loss terms, alongside a latent recovery loss tailored to the specifics of the GAN architecture in question.

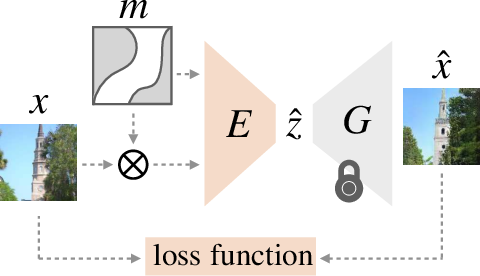
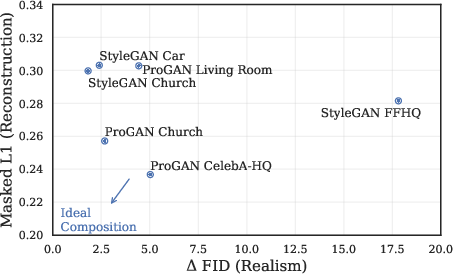
Figure 2: We train a latent space regressor $E$ to predict the latent code $\hat{z}$ that, when passed through a fixed generator, reconstructs input $x$. At training and test time, we can also modify the encoder input with additional binary mask $m$. Inference requires only a forward pass and the input $x$ can be unrealistic, as the encoder and generator serve as a prior to map the image back to the image manifold.

Handling Missing Data

To facilitate inpainting and the blending of image components, the regressor model incorporates a masking mechanism, enabling the network to explicitly handle unknown image regions. This allows the generator to realistically complete scenes with missing parts, preserving the integrity and coherence of the overall scene.

Figure 3: Image completions using the latent space regressor. Given a partial image, a masked regressor realistically reconstructs the scene in a way that is consistent with the given context. The completions (``Inverted'') can vary depending on the exposed context region of the same input.

Experimental Evaluation

Image Composition

The experimental framework involves tasking the networks with recomposing collaged images. These collaged inputs are derived from disparate image parts, and the network must blend, inpaint, and align these inputs into a seamless, realistic output. The results demonstrate the regressor's ability to maintain realism while achieving significant reconstruction fidelity, balancing between these factors effectively across different dataset domains.

Figure 4: Trained only on a masked reconstruction objective, a regressor into the latent space of a pretrained GAN allows the generator to recombine components of its generated images, despite strong misalignments and missing regions in the input. Here, we show automatically generated collaged inputs from extracted image parts and the corresponding outputs of the generators.

Comparison with Baselines

A variety of image reconstruction techniques are compared, including autoencoders and optimization-based methods. These comparisons reveal that GAN-based methods with a regressor are capable of maintaining a balance between realistic outputs and input fidelity, often surpassing other methods in realism and computational efficiency.

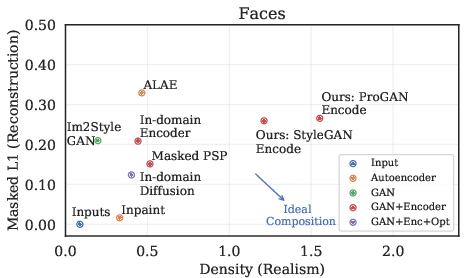
Figure 5: Comparing reconstruction of image collages (masked L1) to realism of the generated outputs on random church collages (left) and face collages (right) across different image reconstruction methods, broadly characterized as autoencoders, GAN-based optimization, GANs with an encoder to perform latent regression, and a combination of GAN, regression, and optimization.

Conclusion

This paper presents a novel use of latent space regression as a tool to explore and exploit the compositional capabilities inherent in pretrained GANs. The paper demonstrates that GANs inherently possess a compositional understanding within their latent spaces, which can be harnessed for various image manipulation and reconstruction tasks without requiring labeled data. This approach opens up avenues for real-time image editing applications, multimodal image synthesis, and the exploration of generative models' inherent biases and priors. Future work could expand on this framework by exploring more sophisticated manipulations and further dissecting the underlying representations encapsulated in the latent space.