Learning Curve Theory (2102.04074v1)

Abstract: Recently a number of empirical "universal" scaling law papers have been published, most notably by OpenAI. `Scaling laws' refers to power-law decreases of training or test error w.r.t. more data, larger neural networks, and/or more compute. In this work we focus on scaling w.r.t. data size $n$. Theoretical understanding of this phenomenon is largely lacking, except in finite-dimensional models for which error typically decreases with $n^{-1/2}$ or $n^{-1}$, where $n$ is the sample size. We develop and theoretically analyse the simplest possible (toy) model that can exhibit $n^{-\beta}$ learning curves for arbitrary power $\beta>0$, and determine whether power laws are universal or depend on the data distribution.

• The paper establishes a theoretical foundation for power-law learning curves by demonstrating how prediction error scales as n⁻ᵝ with increasing data.
• It introduces a toy model with a countable feature space to show how memorization and feature occurrence probabilities, including Zipf-distributed data, drive error predictions.
• The study highlights practical implications for optimizing computational resource allocation and network design, with potential extensions to more complex models.

Theoretical Analysis and Practical Implications of "Learning Curve Theory"

Introduction

"Learning Curve Theory" (2102.04074) presents an analytical framework to understand the power-law scaling observed in learning curves for large-scale machine learning models. Unlike empirical studies which focus on experimental evidence, this paper aims to establish a theoretical foundation that explains how errors decrease with increasing sample size in various learning settings. The core objective is to discern whether power laws are universal characteristics of learning curves or are contingent on specific data distributions.

Power Laws in Machine Learning

Empirical studies have demonstrated that larger models, richer datasets, and greater computational resources lead to improved performances of neural networks (NNs). Observations indicate that the errors or losses show power-law decreases relative to data size, model size, and compute budget, provided that none of these factors bottlenecks the others. This paper specifically addresses the scaling with data size $n$ and examines the theoretical underpinnings of the phenomenon where the error scales as $n^{-\beta}$.

The Toy Model

The paper introduces a toy model with countable feature space for classification tasks, which captures the essential characteristics of observed power-law behaviors. The deterministic model predicts errors based on a simple memorization algorithm: if a feature hasn't been seen before, it results in a prediction error. The error probability is formulated as:

$$\mathbb{E}[\epsilon_n] = \sum_{i=1}^{\infty} \theta_i (1-\theta_i)^n$$

where $\theta_i$ is the occurrence probability of feature $i$. This forms the learning curve as a function of the sample size $n$ and is pivotal for subsequent analysis.

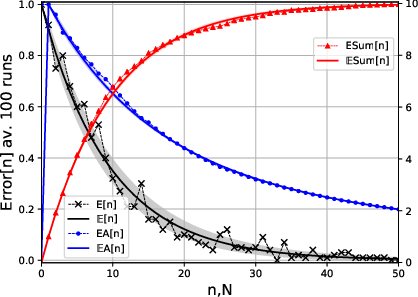
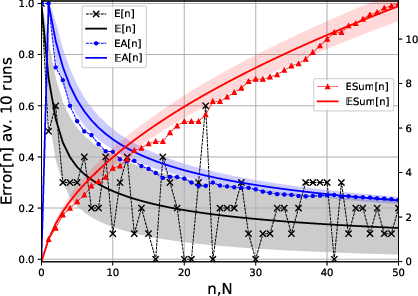
Figure 1: Learning Curves

Analytic Derivations of Learning Curves

The model allows derivation of expected learning curves under various distribution scenarios:

• Exponential Decay: For finite models with equally probable features, the error exhibits exponential decay, approaching not the typical power law form.
• Zipf Distribution: Real data often follows Zipf's law, where the frequency of item occurrences is a power function of its rank. The paper shows that Zipf-distributed data naturally leads to power-law learning curves with exponents that are functions of the distributional parameter.

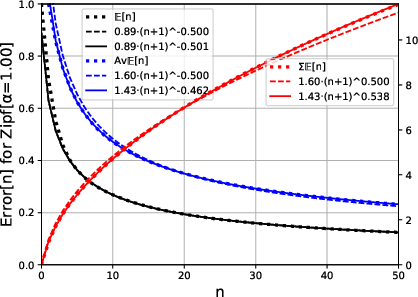
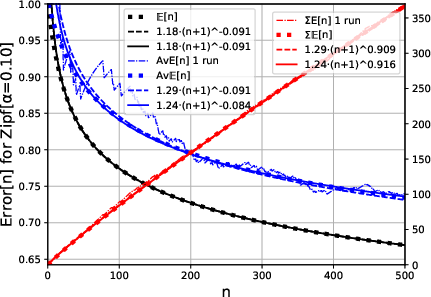
Figure 2: Power Law fit to Zipf-Distributed Data

Insights on Learning Curve Variance

The analysis considers the variance of the learning curves, noting that the signal-to-noise ratio deteriorates with increasing sample size. However, for time-averaged errors, the variance reduces significantly, implying that stable learning curves can be approximated from fewer experimental runs.

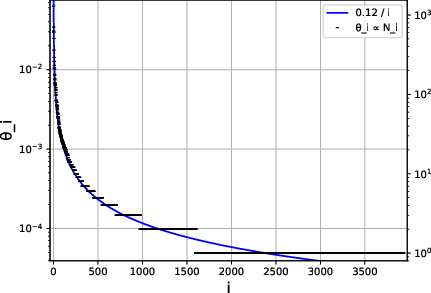
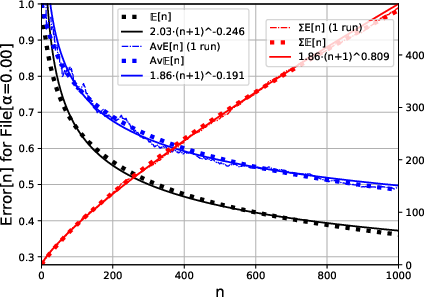
Figure 3: Word-Frequency in Text File, Learning Curve, Power Law

Discussion and Extensions

The work encapsulates the conceptual scaffold for understanding scaling laws beyond mere empirical observations, emphasizing the potential universality of power-law behaviors. It suggests extensions to more complex models and includes discussions on continuous feature spaces and noisy labels.

Practical Implications and Future Work

Understanding these scaling laws can optimize the allocation of computational resources and network architecture decisions, reducing the cost and time of training large models. The toy model's predictions invite further exploration with non-parametric models and deep networks to corroborate these theoretical findings with practical implementations.

Conclusion

The paper lays the groundwork for a systematic theory of scaling laws in machine learning, providing a simplified yet profound tool for explaining and predicting the behavior of learning curves in real-world applications. It invites future research to extend these concepts to more sophisticated models, potentially offering a more robust understanding of the underlying dynamics governing learning in artificial neural networks.