Logic Tensor Networks
Abstract: Artificial Intelligence agents are required to learn from their surroundings and to reason about the knowledge that has been learned in order to make decisions. While state-of-the-art learning from data typically uses sub-symbolic distributed representations, reasoning is normally useful at a higher level of abstraction with the use of a first-order logic language for knowledge representation. As a result, attempts at combining symbolic AI and neural computation into neural-symbolic systems have been on the increase. In this paper, we present Logic Tensor Networks (LTN), a neurosymbolic formalism and computational model that supports learning and reasoning through the introduction of a many-valued, end-to-end differentiable first-order logic called Real Logic as a representation language for deep learning. We show that LTN provides a uniform language for the specification and the computation of several AI tasks such as data clustering, multi-label classification, relational learning, query answering, semi-supervised learning, regression and embedding learning. We implement and illustrate each of the above tasks with a number of simple explanatory examples using TensorFlow 2. Keywords: Neurosymbolic AI, Deep Learning and Reasoning, Many-valued Logic.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What the paper is about
This paper introduces Logic Tensor Networks (LTN), a way to combine two big ideas in Artificial Intelligence:
- Neural networks, which learn from data (like images or text) but don’t usually use clear symbols and rules.
- Logic, which uses rules and symbols (like “for all x” or “if A then B”) to reason in a human-understandable way.
The authors build a “fully differentiable” logical language called Real Logic. That means the logic is designed to work smoothly with the math used to train neural networks. With LTN, you can learn from data and also use rules about the world—both at the same time. They show that this single framework can handle many common AI tasks, and they provide an implementation in TensorFlow 2 with examples.
What questions the paper asks
The paper explores simple, practical questions:
- How can we teach AI systems using both data and human-style rules?
- Can we turn logical statements (like “for all” or “there exists”) into math that neural networks can learn from?
- How do we connect abstract symbols (like “is a cat” or “parentOf”) to real data (like images or numbers)?
- Can we make logical reasoning and neural learning work together without breaking training (no vanishing or exploding gradients)?
- Can one unified approach handle tasks like classification, clustering, regression, relational learning, and answering logical queries?
How the researchers approached the problem
Think of Real Logic as giving every logical statement a “confidence score” between 0 and 1, instead of just true or false. Here’s how they make it work with everyday analogies:
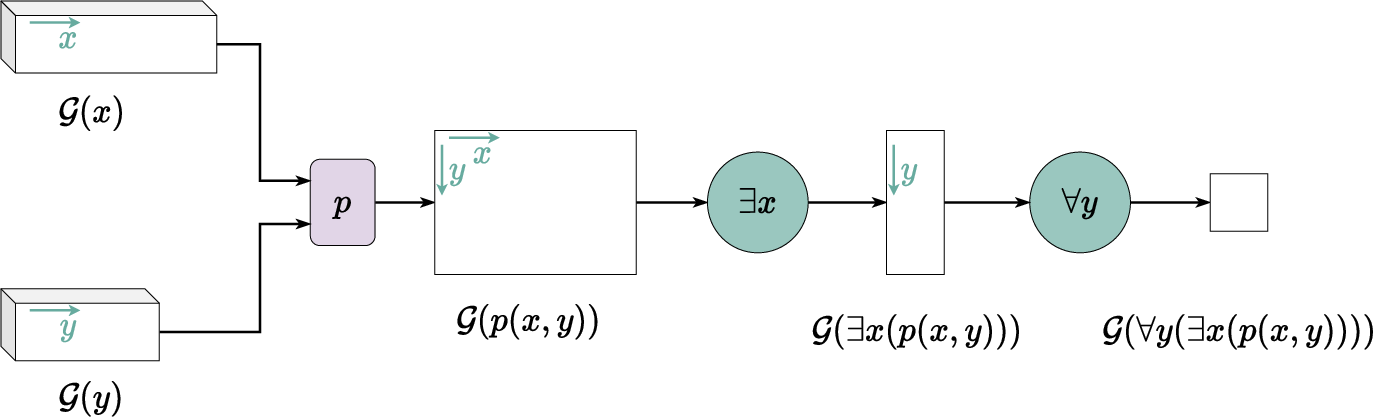
- Grounding symbols into data: In classic logic, symbols are abstract. In Real Logic, every symbol (like a constant, function, or relation) is “grounded” to actual numbers or tensors (multi-dimensional arrays), like an image represented as a big grid of pixels. This is like attaching a “data profile” to each symbol so it connects to reality.
- Truth as a dial from 0 to 1: Instead of saying a statement is strictly true or false, they use fuzzy truth-values (a confidence dial). For example, “this picture is a cat” might be 0.92 true.
- Logical connectives as smooth math:
- AND behaves like multiplying confidences (high only if both are high).
- OR behaves like a smooth combination (high if either is high).
- NOT flips the confidence.
- IF (implication) is made “smooth” so learning stays stable.
- Quantifiers as smart aggregations:
- “For all” (∀) acts like a smooth minimum over many cases—high only if almost all cases are high.
- “There exists” (∃) acts like a smooth maximum—high if at least one case is high.
- These “smooth max/min” are done with special averages that can be tuned, so training remains stable and robust to outliers.
- Diagonal quantification: When you want to pair the i-th item with the i-th label (like each image with its correct label), diagonal quantification checks those pairs only, not all combinations. Imagine matching each student with their own grade rather than mixing everyone’s grades.
- Guarded quantifiers: These let you apply rules only to items that meet a condition. For example, “for all people with age < 10, if they play piano then they are a prodigy.” This is like filtering your dataset first, then applying the rule.
- Stable training tricks: Some logical operations can cause training problems (gradients becoming too small or too large). The authors slightly “nudge” values away from exact 0 or 1 with a tiny epsilon (like adding a cushion), so gradients flow smoothly and training stays stable.
- Learning as satisfiability: Parameters of the neural parts are learned by making the logical statements as “satisfied” as possible. In simple terms: adjust the network so the rules and facts are as true as they can be on the data.
What they found and why it matters
The authors demonstrate that LTN is a flexible, unified way to do many AI tasks while using logical knowledge:
- It can handle multi-label classification, relational learning (learning relationships between things), clustering, semi-supervised learning, regression, embedding learning (mapping symbols into vectors), and answering logical queries.
- The framework handles rich, human-readable rules alongside deep learning, making models more understandable and able to use prior knowledge.
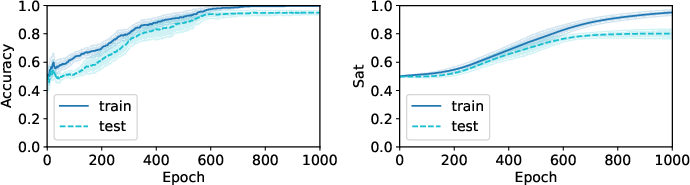
- Their “stable product” setup for logic operators and their smooth quantifiers help avoid training issues like vanishing or exploding gradients.
- They add useful features to make logic practical in machine learning:
- Typed domains (e.g., person vs. city), so symbols stay organized.
- Guarded and diagonal quantification, so you can target the right subsets or matched pairs easily.
- They also define a formal way to do refutation-based reasoning (checking whether a statement follows from a knowledge base), which they show captures logical consequences better than naive querying after training.
Overall, their examples in TensorFlow 2 suggest LTN is both general and powerful for mixing rules with learning.
What this could mean in the future
LTN pushes AI toward systems that can learn from data while also following human-style rules. This has several potential benefits:
- Better use of limited or noisy data by injecting knowledge (rules) to guide learning.
- More interpretable models that can explain decisions using logical statements.
- Stronger generalization beyond the training set, because rules capture structure that data alone might miss.
- A single “language” to describe and solve different AI tasks, making systems easier to build and maintain.
In short, Logic Tensor Networks offer a practical path to neurosymbolic AI—combining the power of neural networks with the clarity and structure of logic.
Collections
Sign up for free to add this paper to one or more collections.