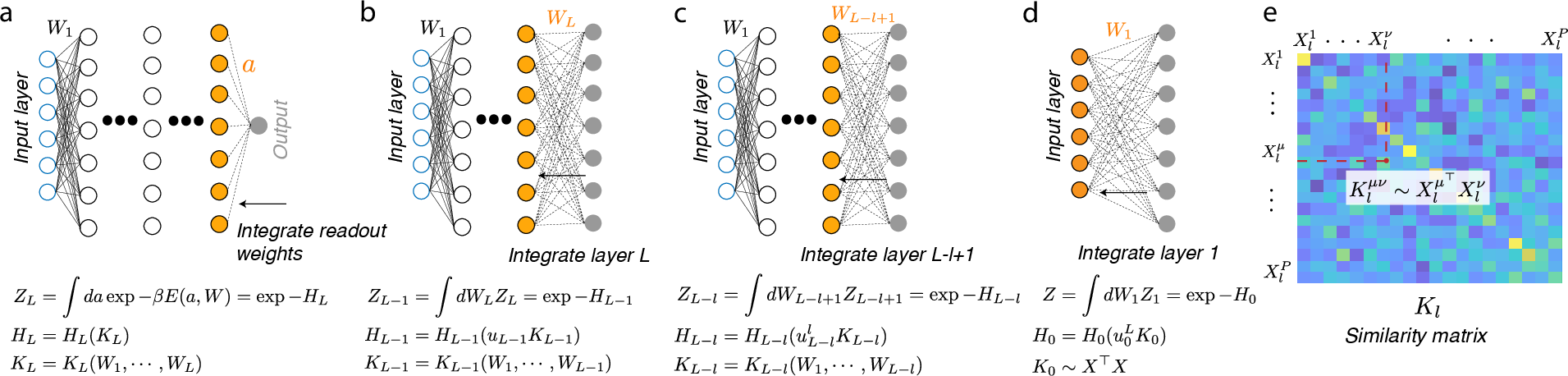Statistical Mechanics of Deep Linear Neural Networks: The Back-Propagating Kernel Renormalization (2012.04030v2)

Abstract: The success of deep learning in many real-world tasks has triggered an intense effort to understand the power and limitations of deep learning in the training and generalization of complex tasks, so far with limited progress. In this work, we study the statistical mechanics of learning in Deep Linear Neural Networks (DLNNs) in which the input-output function of an individual unit is linear. Despite the linearity of the units, learning in DLNNs is nonlinear, hence studying its properties reveals some of the features of nonlinear Deep Neural Networks (DNNs). Importantly, we solve exactly the network properties following supervised learning using an equilibrium Gibbs distribution in the weight space. To do this, we introduce the Back-Propagating Kernel Renormalization (BPKR), which allows for the incremental integration of the network weights starting from the network output layer and progressing backward until the first layer's weights are integrated out. This procedure allows us to evaluate important network properties, such as its generalization error, the role of network width and depth, the impact of the size of the training set, and the effects of weight regularization and learning stochasticity. BPKR does not assume specific statistics of the input or the task's output. Furthermore, by performing partial integration of the layers, the BPKR allows us to compute the properties of the neural representations across the different hidden layers. We have proposed an extension of the BPKR to nonlinear DNNs with ReLU. Surprisingly, our numerical simulations reveal that despite the nonlinearity, the predictions of our theory are largely shared by ReLU networks in a wide regime of parameters. Our work is the first exact statistical mechanical study of learning in a family of DNNs, and the first successful theory of learning through successive integration of DoFs in the learned weight space.

• The paper presents the Back-Propagating Kernel Renormalization method which exactly analyzes DLNNs by integrating weights layerwise as an equilibrium statistical mechanics problem.
• This method reveals the interplay between depth, width, training sample size, and regularization, critically influencing generalization error in over-parameterized regimes.
• Extensions to nonlinear networks with ReLU units suggest that the BPKR framework could inform optimized architecture design in practical deep learning applications.

Statistical Mechanics of Deep Linear Neural Networks: The Back-Propagating Kernel Renormalization

Introduction

This paper explores the statistical mechanics underlying deep linear neural networks (DLNNs), where individual units follow a linear input-output function. Despite these linear characteristics, learning within DLNNs introduces non-linearity due to the multiplicative interactions among weights. This research advances our understanding by proposing the Back-Propagating Kernel Renormalization (BPKR) framework, offering an exact analysis of DLNN properties post-supervised learning.

Figure 1: Schematics of the Back-Propagating Kernel Renormalization demonstrating layer-by-layer integration of weights.

Back-Propagating Kernel Renormalization

The crux of the analysis utilizes an exact technique for studying neural network properties by treating the learning process as an equilibrium statistical mechanics problem in the DLNN weight space. The BPKR method involves progressive integration of weights starting from the output layer and proceeding backward to the input layer. This integration exploits the properties of Gibbs distribution and introduces an effective kernel renormalization at each layer, fundamentally linking network characteristics such as generalization and the interplay of depth, width, and the size of training samples.

Implementation Considerations

Implementing this kernel renormalization technique centers around successive backward integration of network weights. The method requires computing the Gibbs distribution's partition function and tackling the renormalization by scalars or matrices depending on the network's architecture (single or multiple outputs). This results in evaluating important metrics such as generalization error and understanding the influence of architectural parameters, regularization, and data characteristics.

Generalization and Analytic Insights

The generalization capabilities of DLNNs, as derived via BPKR, reveal a complex interplay of factors. For instance, networks display varying generalization performance based on noise levels and the width of layers, showing possibilities of achieving superior performance in over-parameterized regimes—a counter-intuitive result suggestive of the power in appropriately regularized deep networks. This analysis highlights regimes where increasing depth or width yields improvements in generalization error, nuanced by the setting of parameters like weight noise and the $L_2$ regularization effects, which can be seen in practical scenarios involving varying sample sizes and network configurations.

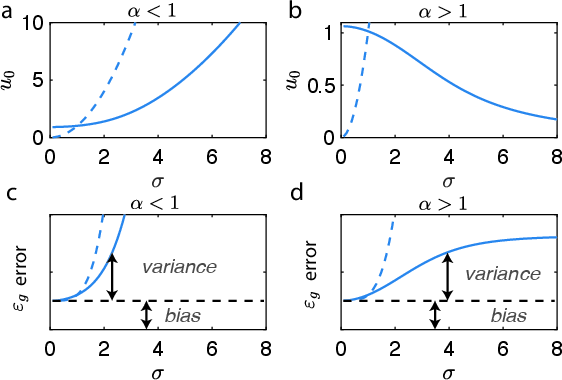
Figure 2: The dependence of the order parameter $u_0$ on network parameters showing distinct behavior in narrow vs wide networks.

Extensions to Nonlinear Networks

Although the primary focus lies on linear architectures, a heuristic expansion of the concepts to nonlinear DNNs with ReLU units is proposed. Despite the simplicity, this extension exhibits surprising congruence with empirical behavior in ReLU networks of moderate depth under specific parameter regimes. Importantly, the theoretical foundations laid by BPKR provide a scaffold that could accommodate more sophisticated analyses of nonlinear networks through potential approximations of kernel renormalization beyond scalar factors.

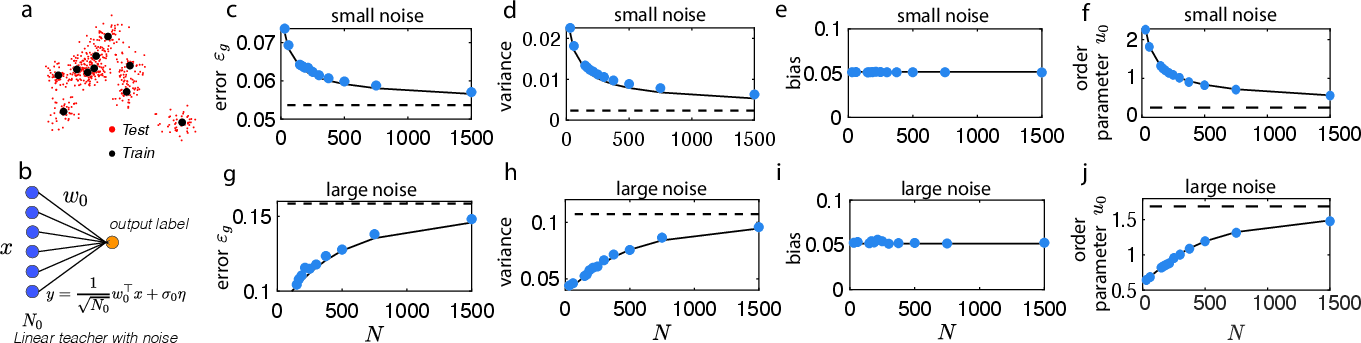
Figure 3: Variance and bias contributions to the generalization error for varying network architectures.

Conclusion

This study provides the first exact statistical mechanical framework for analyzing learning in DLNNs via the groundbreaking Back-Propagating Kernel Renormalization method. The implications extend to understanding generalization in the over-parameterized field of deep learning, offering a granular analytic perspective on layerwise representations and generalization dynamics. Future explorations could further bridge these insights with practical deployment strategies in networks tasked with complex, real-world functionalities, potentially adapting BPKR concepts to diverse nonlinear scenarios.

The work thus bridges the gap between theoretical predictions and practical architecture design in neural networks, illuminating paths for optimized network construction and comprehension of deep learning’s inherent capabilities and constraints.