Physics-informed neural networks for myocardial perfusion MRI quantification (2011.12844v3)

Abstract: Tracer-kinetic models allow for the quantification of kinetic parameters such as blood flow from dynamic contrast-enhanced magnetic resonance (MR) images. Fitting the observed data with multi-compartment exchange models is desirable, as they are physiologically plausible and resolve directly for blood flow and microvascular function. However, the reliability of model fitting is limited by the low signal-to-noise ratio, temporal resolution, and acquisition length. This may result in inaccurate parameter estimates. This study introduces physics-informed neural networks (PINNs) as a means to perform myocardial perfusion MR quantification, which provides a versatile scheme for the inference of kinetic parameters. These neural networks can be trained to fit the observed perfusion MR data while respecting the underlying physical conservation laws described by a multi-compartment exchange model. Here, we provide a framework for the implementation of PINNs in myocardial perfusion MR. The approach is validated both in silico and in vivo. In the in silico study, an overall reduction in mean-squared error with the ground-truth parameters was observed compared to a standard non-linear least squares fitting approach. The in vivo study demonstrates that the method produces parameter values comparable to those previously found in literature, as well as providing parameter maps which match the clinical diagnosis of patients.

• The paper demonstrates that physics-informed neural networks (PINNs) can accurately estimate myocardial blood flow by integrating tracer-kinetic models.
• It leverages ordinary differential equations from a two-compartment model to enforce physiological constraints and reduce error margins.
• Validation with both digital phantoms and patient data highlights PINNs’ potential for non-invasive cardiac diagnostics.

Physics-Informed Neural Networks for Myocardial Perfusion MRI Quantification

Introduction

The paper "Physics-informed neural networks for myocardial perfusion MRI quantification" (2011.12844) explores the application of physics-informed neural networks (PINNs) to myocardial perfusion magnetic resonance imaging (MRI). In this context, PINNs are utilized to infer tracer-kinetic parameters, leveraging the inherent physical laws governed by multi-compartment exchange models. The primary goal is to offer a robust framework that adheres to physiological principles, providing reliable quantification of myocardial blood flow (MBF) and other microvascular functions.

Tracer-Kinetic Modelling

Tracer-kinetic models play a crucial role in delineating the transport dynamics of contrast agents across tissue compartments, specifically the plasma and interstitial space, as described by the two-compartment exchange model (2CXM). This model is defined through ordinary differential equations that characterize the variation of contrast agent concentration in these compartments over time. The neural network framework aims to approximate the solution to these equations and identify the MBF and other parameters like plasma volume (vp) and permeability-surface area (PS).

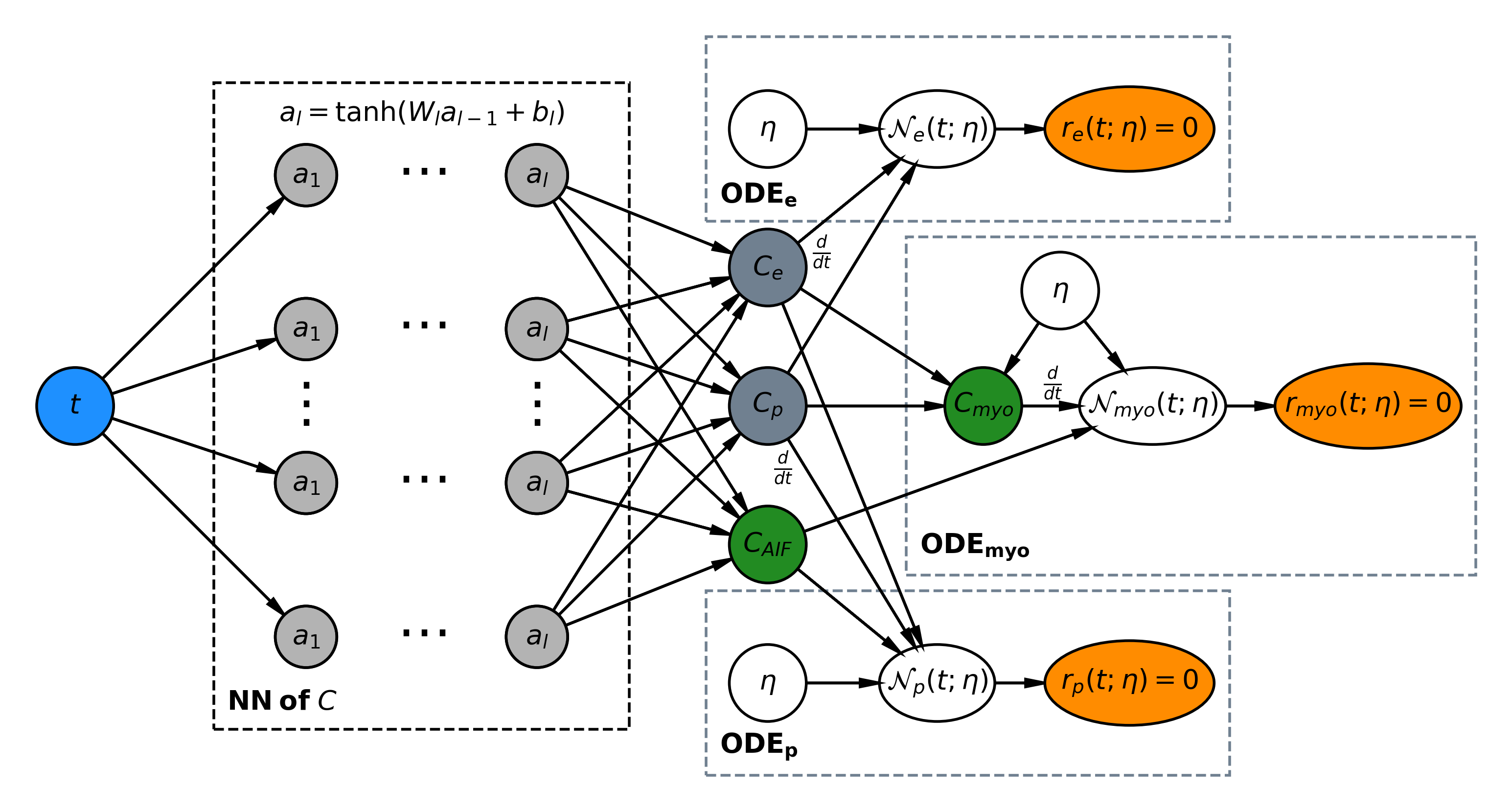
Figure 1: A schematic representation of the physics-informed neural network for myocardial perfusion, integrating contrast agent fitting to modulate neural network behavior.

Physics-Informed Neural Networks

PINNs represent an innovative approach within deep learning, addressing parameter estimation by inferring solutions that respect the underlying physical laws specified by differential equations. Unlike conventional machine learning models, PINNs embed the physics of the problem, resulting in outputs consistent across the temporal domain, further augmented by the ability to compute loss not only at the measurement points but at any time domain point to enhance model fit and predictive accuracy.

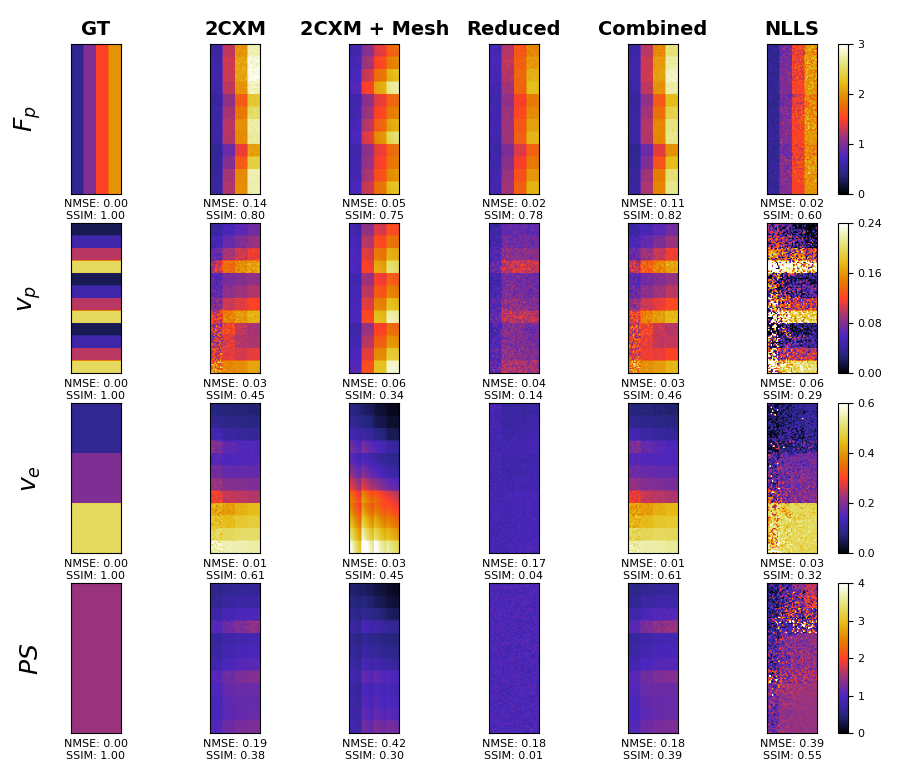
Figure 2: Results from the digital phantom paper comparing parameter inference methods, illustrating PINNs' superior performance.

Experiments and Results

Experiments conducted in the paper include both in silico and in vivo validations to compare the performance of PINNs against standard non-linear least squares (NLLS) techniques. In the in silico domain, PINNs demonstrated reduced mean-squared errors when mapping against ground-truth parameters. Practically, patient data analysis exhibited acceptable MBF value ranges in line with clinical expectations, underscoring PINNs' promise in diagnostic scenarios.

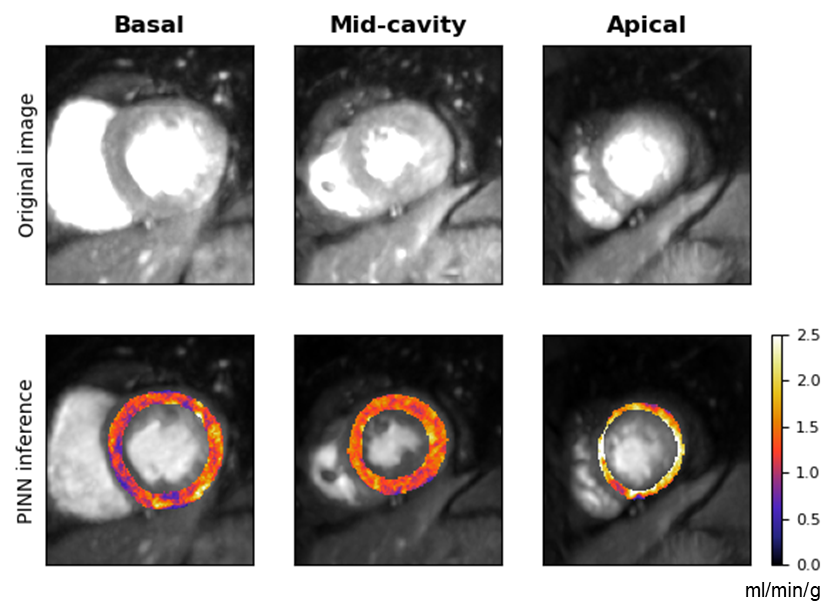
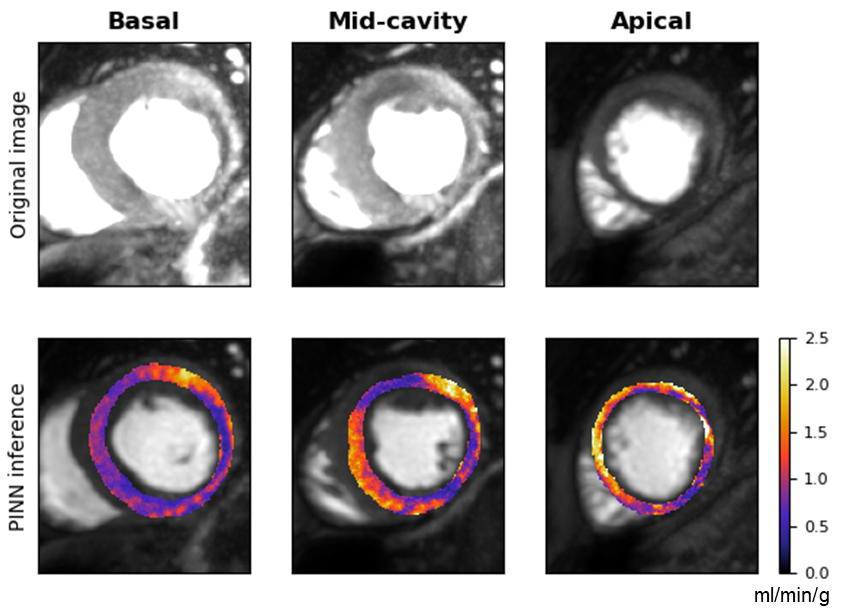
Figure 3: Estimated MBF maps showing distinct perfusion profiles for patients with and without notable coronary artery disease.

Discussion

Aside from the reduction in error margins, PINNs offer significant flexibility, allowing incorporation of spatial dependencies and a multi-modal loss framework that includes observation data, boundary conditions, and regularised non-negative constraints. This flexibility is pivotal for tackling the inherent complexity of myocardial perfusion modelling and retaining structural integrity in inferred parameter values. Moreover, PINNs' efficiency stems from leveraging data-driven optimization strategies that mitigate local optima challenges, a frequent pitfall in model-based regression approaches.

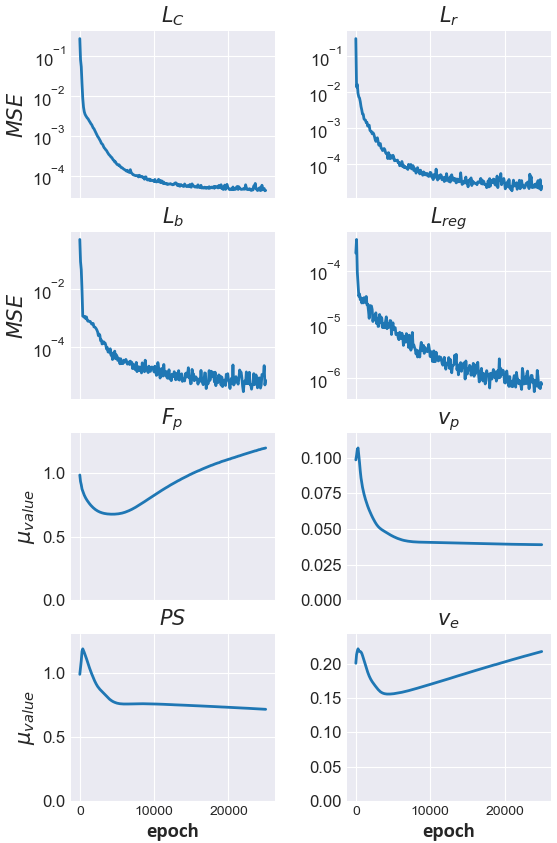
Figure 4: Training curves illustrating loss evolution and parameter estimate stabilization throughout the optimization process.

Conclusion

This research highlights the feasibility and advantage of employing physics-informed neural networks in the domain of myocardial perfusion quantification. The promising results advocate for further exploration into PINNs as a mainstay for kinetic parameter estimation in cardiac MRI, potentially redefining non-invasive cardiac diagnostics through enhanced data-efficiency and model robustness.

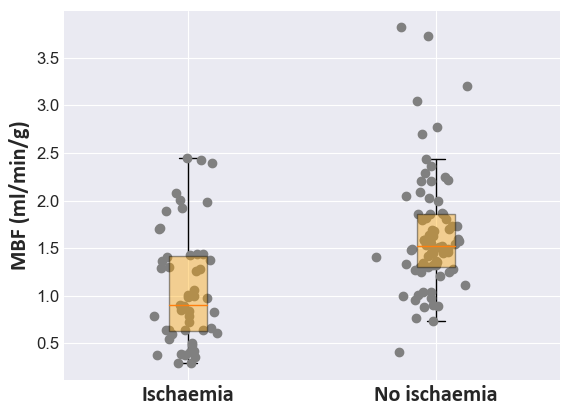
Figure 5: Distribution analysis of inferred MBF values distinguishing ischemic from non-ischemic segments, validating diagnostic accuracy.

In summary, PINNs integrate physiological modelling and deep learning practices to overcome traditional barriers in tracer-kinetic analysis, granting both theoretical and practical advancement in cardiovascular imaging technology. Future work should focus on accelerating computational execution and further exploring PINNs' application breadth within tracer-kinetic frameworks.