AML-SVM: Adaptive Multilevel Learning with Support Vector Machines (2011.02592v1)

Abstract: The support vector machines (SVM) is one of the most widely used and practical optimization based classification models in machine learning because of its interpretability and flexibility to produce high quality results. However, the big data imposes a certain difficulty to the most sophisticated but relatively slow versions of SVM, namely, the nonlinear SVM. The complexity of nonlinear SVM solvers and the number of elements in the kernel matrix quadratically increases with the number of samples in training data. Therefore, both runtime and memory requirements are negatively affected. Moreover, the parameter fitting has extra kernel parameters to tune, which exacerbate the runtime even further. This paper proposes an adaptive multilevel learning framework for the nonlinear SVM, which addresses these challenges, improves the classification quality across the refinement process, and leverages multi-threaded parallel processing for better performance. The integration of parameter fitting in the hierarchical learning framework and adaptive process to stop unnecessary computation significantly reduce the running time while increase the overall performance. The experimental results demonstrate reduced variance on prediction over validation and test data across levels in the hierarchy, and significant speedup compared to state-of-the-art nonlinear SVM libraries without a decrease in the classification quality. The code is accessible at https://github.com/esadr/amlsvm.

Adaptive Multilevel Learning with SVMs: Methodology, Analysis, and Implications

Introduction and Problem Context

Nonlinear Support Vector Machines (SVMs) remain highly effective for complex classification tasks due to their flexibility and theoretical robustness. However, the practical use of nonlinear SVMs with large-scale data sets is hindered by their computational and memory complexity. The core challenge arises from the quadratic scaling of kernel matrix construction and solver complexity with the sample size, making standard SVM strategies intractable for massive datasets. Parameter optimization further exacerbates this, particularly for high-dimensional or imbalanced datasets.

The Adaptive Multilevel Learning (AML-SVM) Framework

The authors propose an adaptive multilevel learning framework for SVMs (AML-SVM), extending the previously established Multilevel SVM (MLSVM) paradigm. This scheme introduces hierarchical learning with adaptive refinement during the uncoarsening phase to both accelerate training and mitigate prediction quality inconsistencies observed in standard multilevel workflows.

The high-level AML-SVM scheme can be summarized as follows:

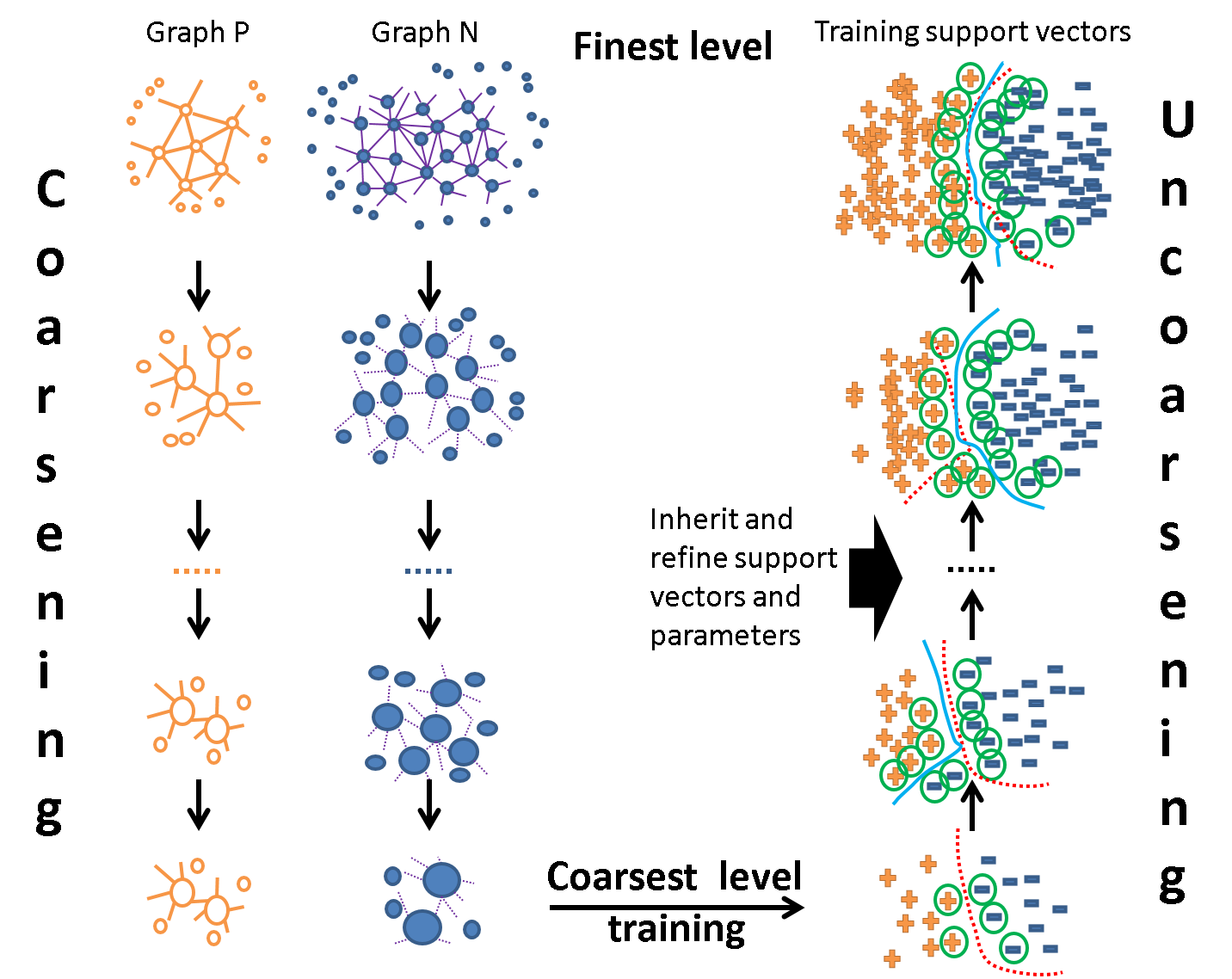
Figure 1: AML-SVM framework: coarsening (aggregation), coarsest-level solution, and adaptive uncoarsening with quality recovery and early stopping.

Coarsening: The dataset is recursively aggregated using an algebraic multigrid (AMG) approach based on kNN proximity graphs, constructing a hierarchy in which each coarser level contains representative aggregates of finer data.

Coarsest-level Solution: The smallest subproblem, now of tractable size, is solved using a high-quality SVM solver with hyperparameter tuning. Instance and class imbalance are modeled via a weighted SVM objective adjusted by point "volumes" (i.e., importance from original data participation).

Uncoarsening (Refinement): The learned parameters and support vectors are interpolated and projected onto finer levels. Critically, AML-SVM integrates two novel strategies:

• Adaptive Detection/Recovery: At each level, model quality is validated using finest-level data. Significant drops in G-mean trigger a recovery subroutine: neighbors of misclassified validation data are augmented into the training set, and the SVM is retrained.
• Early Stopping: If the required training set at fine levels exceeds a computational threshold or quality plateaus, refinement is halted to avoid unnecessary cost.

Addressing Quality Degradation Across Levels

An important observation motivating adaptation is that the natural expectation of monotonic improvement of classification quality during refinement is often violated. Instead, on some benchmarks, intermediate levels yield marked drops in quality that persist and compound at finer resolutions. This is visualized in a contrast between "natural" and "unnatural" refinement trajectories:

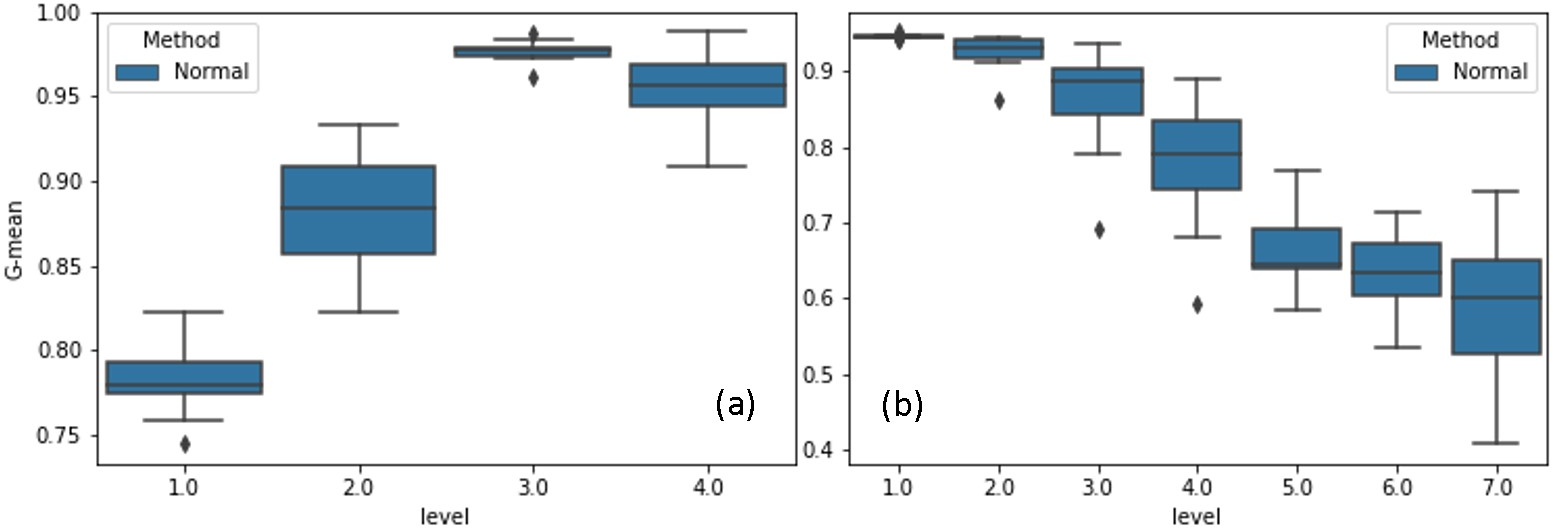
Figure 2: (a) Natural trend — increasing G-mean at each finer level; (b) Unnatural trend — decreasing/intermittent recovery in G-mean, necessitating adaptive recovery.

Mechanism of Quality Drop: Suboptimal support vectors or over-filtered aggregation can exclude essential decision boundary information, particularly in the presence of class imbalance or feature redundancy, causing further levels to train on unrepresentative data.

Recovery Approach: Upon quality drop detection, AML-SVM augments the training data at a given level by adding nearest neighbors of misclassified validation points, thus localizing the model’s corrective updates near challenging decision boundaries without inflating training size uncontrollably.

Experimental Analysis: Numerical Efficacy and Efficiency

The numerical results across multiple benchmarks, including large UCI datasets and synthetics, establish several strong claims:

• Speedup: AML-SVM achieves up to two orders of magnitude reduction in wall-time compared to state-of-the-art nonlinear SVM libraries, especially as compared to LIBSVM and DC-SVM, without loss of test-set G-mean.
• Prediction Quality: The maximal G-mean obtained by the AML-SVM is at least as high as regular MLSVM and baseline solvers, typically improving over LIBSVM/DC-SVM. The adaptive phase reduces inter-level variance and consistently recovers from quality dips.
• Early Stopping: On datasets where overfitting is correlated with growing training set size at fine levels, early stopping yields further runtime reductions and guards against spurious complexity increase.
• Parallel Hyperparameter Fitting: Multi-threaded NUD parameter search at each level provides significant wall-time improvements, making the AML-SVM practically feasible for millions of samples.

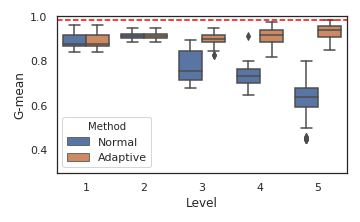
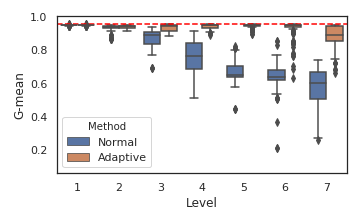
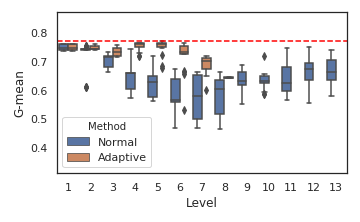
Figure 3: G-mean trends across hierarchical levels for Clean, Cod, and SUSY datasets, illustrating adaptive quality recovery and variance reduction.

Additional Illustrative Experiments: Data Distribution Effects

The generalization performance of AML-SVM under synthetic data was tested using structured 3D and 2D grids, showing that even under distributional shift (test grid generated with slightly altered covariance), hierarchical and adaptive learning continue to outperform conventional approaches and competing multilevel frameworks.

Figure 4: Synt1—3D grid data, used in synthetic benchmarking of scalability and decision boundary recovery.

Figure 5: Synt1, 2D grid projection for visualization of boundary structure and class arrangement.

Figure 6: Synt1, test set distribution showing AML-SVM robustness to subtle distributional change.

Implementation Considerations

• Memory and Computation: The most memory-intensive step, kernel matrix construction, is confined to coarser levels. Only a subset of data near support vectors is used for refinement at finer levels, rendering the method highly scalable.
• Imbalanced Data: The independent coarsening and volume-based weighting ensure that minority classes are not eliminated during aggregation, and adaptive validation sampling is tailored further for class representation.
• Feature Space and kNN Graphs: The critical hyperparameter $k$ in kNN graph construction influences the trade-off between computation (for larger $k$) and neighborhood granularity. Empirical tuning is dataset-dependent but robust around $k=10$.
• Parallelization and Solver Flexibility: The framework modularizes to allow integration of fast GPU solvers or more complex SVM variants; the main algorithm can leverage advanced hardware directly for further gains.

Implications and Future Work

Theoretical Expansion: AML-SVM establishes that hierarchical, instance-adaptive approaches can maintain—if not strengthen—the global optimum-seeking property of SVMs even in highly challenging, large, or imbalanced regimes. The consistent observation that optimal or near-optimal classifiers often appear at intermediate rather than the finest levels suggests new directions for regularization theory and layout of ensemble methods using multi-coarsened models.

Practical Adaptability: The framework presents a substantial improvement in the cost-accuracy frontier for nonlinear SVMs, making the use of interpretable models feasible in domains currently dominated by deep learners purely for scalability reasons. Efficient imbalanced learning and resistance to overfitting extend its applicability to high-stakes fields such as computational biology, fraud detection, and process monitoring.

Ensembles and Model Selection: The insight that models at multiple granularities can exhibit equivalent test-set performance may fuel the design of hierarchical ensembling or automated model selection pipelines capable of balancing accuracy and efficiency dynamically.

Transfer and Meta-learning: Adaptive validation and parameter inheritance in the AML-SVM framework can inform techniques for transfer learning, meta-optimization, and explainable AI, where hierarchical adaptation is desirable and critical for practical deployment.

Conclusion

AML-SVM constitutes a definitive advancement in scalable kernel SVM training for large and imbalanced data, leveraging an adaptive multilevel learning strategy to enforce monotonic quality improvement, reduce computational burden, and provide robust predictions with minimal tuning sensitivity. The framework’s extensibility to heterogeneous computation and its demonstrated empirical superiority make it a strong candidate for future-standard SVM toolkits in both research and industry deployments.