Model Predictive Contouring Control for Collision Avoidance in Unstructured Dynamic Environments (2010.10190v1)

Abstract: This paper presents a method for local motion planning in unstructured environments with static and moving obstacles, such as humans. Given a reference path and speed, our optimization-based receding-horizon approach computes a local trajectory that minimizes the tracking error while avoiding obstacles. We build on nonlinear model-predictive contouring control (MPCC) and extend it to incorporate a static map by computing, online, a set of convex regions in free space. We model moving obstacles as ellipsoids and provide a correct bound to approximate the collision region, given by the Minkowsky sum of an ellipse and a circle. Our framework is agnostic to the robot model. We present experimental results with a mobile robot navigating in indoor environments populated with humans. Our method is executed fully onboard without the need of external support and can be applied to other robot morphologies such as autonomous cars.

• The paper introduces LMPCC, an extension to MPCC that unifies motion planning and control for effective collision avoidance in dynamic settings.
• It utilizes convex free-space partitioning and Kalman filter predictions to dynamically manage static and moving obstacles.
• Simulations and real-world tests show improved efficiency, reduced path deviations, and reliable performance across various robotic kinematic models.

Model Predictive Contouring Control for Collision Avoidance in Unstructured Dynamic Environments

The paper introduces a novel approach for local motion planning in dynamic environments with both static and moving obstacles, leveraging an extension of Model Predictive Contouring Control (MPCC), termed Local MPCC (LMPCC), designed to cater to the complexities of autonomous navigation in unstructured settings. This framework circumvents traditional separations between motion planning and control, unifying them into a single optimization-based receding-horizon approach that not only minimizes tracking errors along a reference path but also ensures collision-free trajectories in dynamic settings.

Architecture and Methodology

The primary contribution of the paper is the incorporation of a static map and dynamic obstacle avoidance in the MPCC framework, modeled as ellipsoids to capture the bounds of the collision region accurately through a conservative approximation using the Minkowski sum. The LMPCC method dynamically divides the prediction horizon into convex free-space regions (Figure 1), allowing for real-time adjustments to navigational paths as environmental conditions change.

Figure 1: Representation of the convex free space (orange squares) around each prediction step on the prediction horizon (purple line) with respect to the inflated static environment and the collision space of the dynamic obstacle (green ellipses) with respect to the vehicle representing discs (blue).

The dynamic avoidance strategy involves predicting future positions of moving obstacles and adjusting control commands in advance. The proposed method uses a robust mathematical model to compute optimal trajectories for collision-free navigation, catering to various robot morphologies including both unicycle and bicycle kinematic models.

Static and Dynamic Collision Avoidance

The static collision avoidance is achieved by creating a parameterizable map of the environment based on a dataset of known obstacles. For dynamic environments, the moving obstacles are treated with a linear Kalman filter forecast, providing expected trajectories for following prediction steps. The elliptical models of dynamic obstacles (Figure 2) ensure that the collision safety boundaries are adequately maintained without overburdening the computational resources.

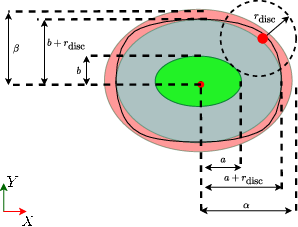
Figure 2: Safety boundary computation. The ellipsoid with semi-major axis and semi-minor axis, a and b respectively, is represented in green, the ellipsoid with axis enlarged by $r_{\text{disc}}$.

Implementation and Performance

The LMPCC framework was tested both in simulation and practical scenarios using a mobile robot equipped for autonomous navigation in indoor environments populated with static obstacles and humans. The framework demonstrated significant improvement in collision avoidance when compared with traditional Model Predictive Control (MPC) approaches and other baseline solutions such as the Dynamic Window approach and socially-aware planners.

Notably, under the LMPCC method, the robot navigates complex environments with improved efficiency marked by reduced path deviations and fewer interactions with obstacles while maintaining real-time computational feasibility, as illustrated by the computation time analysis (Figure 3).

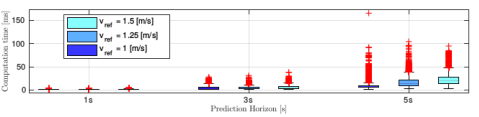
Figure 3: Computation time required to solve the LMPCC problem online for different velocity references and horizon lengths.

Practical Implications and Future Work

The MPCC extension promises a superior approach for real-world navigation challenges faced by autonomous platforms operating in unpredictable and dynamic settings, including urban environments where interaction with pedestrians and dynamically changing obstacles are common.

Future research directions may involve scaling the method for crowded scenarios, enhancing interaction modeling based on the observed behaviors of adjacent entities, and integrating a learning-based approach for improved predictive accuracy. Additionally, enhancing the robustness of dynamic collision avoidance in high-density environments remains an open challenge worth exploring.

Conclusion

The paper presents a comprehensive and effective solution for local motion planning using the LMPCC model, ensuring safety and optimality in dynamic and unstructured environments. This research demonstrates potential applications across various domains involving autonomous vehicle navigation, with practical implementations proving the effectiveness of the proposed framework.