Self-Adaptive Physics-Informed Neural Networks using a Soft Attention Mechanism (2009.04544v5)

Abstract: Physics-Informed Neural Networks (PINNs) have emerged recently as a promising application of deep neural networks to the numerical solution of nonlinear partial differential equations (PDEs). However, it has been recognized that adaptive procedures are needed to force the neural network to fit accurately the stubborn spots in the solution of "stiff" PDEs. In this paper, we propose a fundamentally new way to train PINNs adaptively, where the adaptation weights are fully trainable and applied to each training point individually, so the neural network learns autonomously which regions of the solution are difficult and is forced to focus on them. The self-adaptation weights specify a soft multiplicative soft attention mask, which is reminiscent of similar mechanisms used in computer vision. The basic idea behind these SA-PINNs is to make the weights increase as the corresponding losses increase, which is accomplished by training the network to simultaneously minimize the losses and maximize the weights. In addition, we show how to build a continuous map of self-adaptive weights using Gaussian Process regression, which allows the use of stochastic gradient descent in problems where conventional gradient descent is not enough to produce accurate solutions. Finally, we derive the Neural Tangent Kernel matrix for SA-PINNs and use it to obtain a heuristic understanding of the effect of the self-adaptive weights on the dynamics of training in the limiting case of infinitely-wide PINNs, which suggests that SA-PINNs work by producing a smooth equalization of the eigenvalues of the NTK matrix corresponding to the different loss terms. In numerical experiments with several linear and nonlinear benchmark problems, the SA-PINN outperformed other state-of-the-art PINN algorithm in L2 error, while using a smaller number of training epochs.

• The paper proposes a novel SA-PINN method that uses trainable soft attention weights to improve accuracy in solving stiff PDEs.
• It integrates Gaussian Process regression with SGD to adaptively weight challenging regions, reducing training epochs and L2 errors.
• NTK analysis reveals that adaptive weights balance the eigenvalue spectrum, thereby enhancing stability and convergence during training.

Self-Adaptive Physics-Informed Neural Networks using a Soft Attention Mechanism

Introduction

The paper "Self-Adaptive Physics-Informed Neural Networks using a Soft Attention Mechanism" introduces a novel adaptation of Physics-Informed Neural Networks (PINNs), aimed at enhancing their ability to solve partial differential equations (PDEs), particularly those that exhibit stiffness. Stiff PDEs are characterized by sharp gradients or rapid changes, which pose challenges for traditional PINN approaches. The proposed method leverages trainable weights that function as a soft attention mechanism, allowing the network to focus on difficult regions of the solution space dynamically. This essay details the methodology, numerical experiments, and theoretical implications presented in the paper.

Methodology

The Self-Adaptive PINNs (SA-PINNs) introduce a framework where weights, analogous to attention masks used in computer vision, are applied adaptively at each training point. These weights adjust dynamically during training, focusing computational resources on regions of the solution with higher errors. The adaptation mechanism is formalized by training the network to minimize losses while simultaneously maximizing the self-adaptation weights. The interplay between loss minimization and weight maximization creates a saddle-point optimization problem, where the neural network effectively 'learns' which parts of the domain require more attention.

The methodology includes Gaussian Process regression to construct a continuous map of these adaptive weights, which facilitates the use of stochastic gradient descent (SGD) for training. This approach is particularly beneficial in cases where standard gradient descent is insufficient due to the complexity of the PDEs being solved.

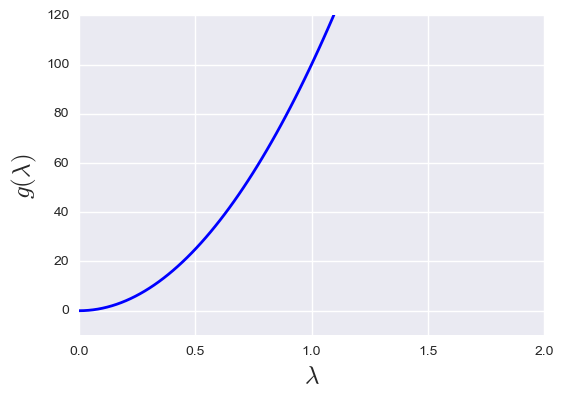
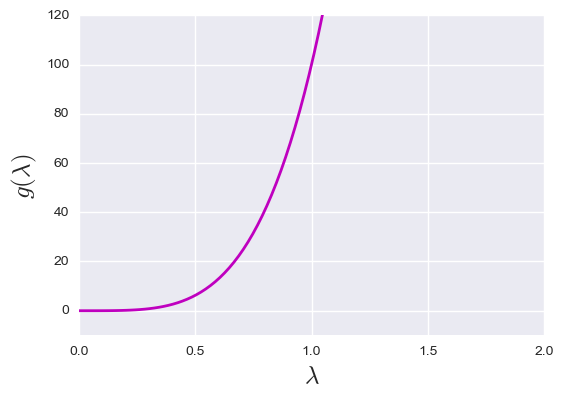
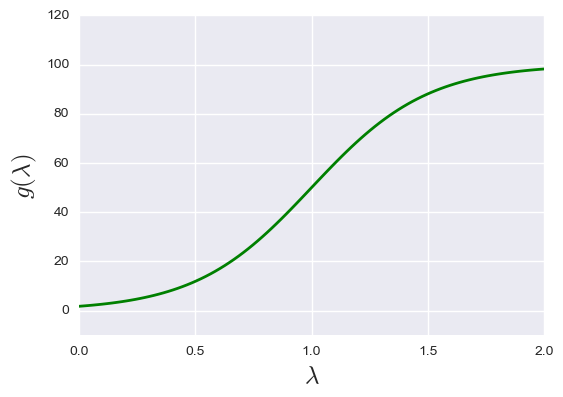
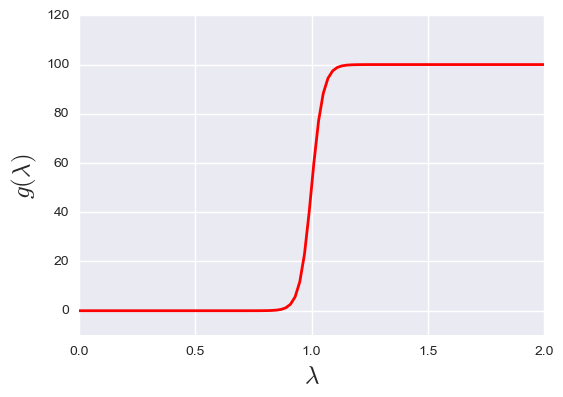
Figure 1: Mask function examples. From the upper left to the bottom right: polynomial mask, $q=2$; polynomial mask, $q=4$; smooth logistic mask; sharp logistic mask.

Numerical Experiments

The paper conducts extensive numerical experiments on several benchmark PDEs to evaluate the performance of SA-PINNs. These experiments highlight the superior accuracy and efficiency of SA-PINNs compared to traditional and state-of-the-art PINN algorithms.

Viscous Burgers Equation

SA-PINNs demonstrated significant improvements in solving the viscous Burgers equation, achieving lower L2 errors in fewer training epochs compared to standard PINNs. The self-adaptive weights concentrated on the shock region of the solution, evident from the larger weights assigned in those areas.

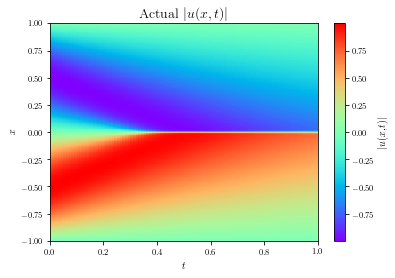
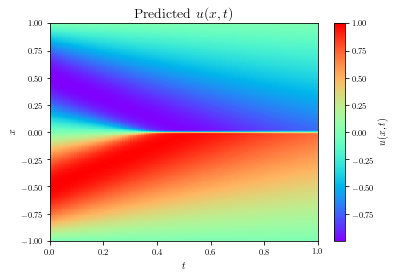
Figure 2: High-fidelity (left) vs. predicted (right) solutions for the viscous Burgers PDE.

Helmholtz Equation

For the Helmholtz equation, the SA-PINNs accurately captured the sinusoidal pattern of the solution, outperforming previous methods like learning-rate annealing. The self-adaptation mechanism enabled efficient learning across the spatial domain, focusing on regions with higher error accumulation.

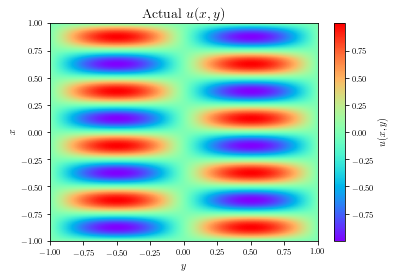
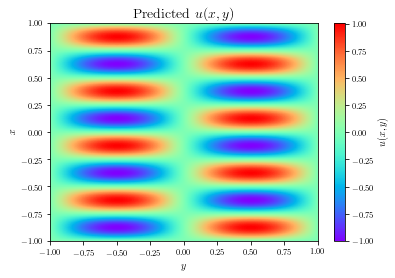
Figure 3: Exact (left) vs. predicted (right) solutions for the Helmholtz PDE.

Theoretical Insights

The paper extends its investigation into the theoretical underpinnings of SA-PINNs by deriving the Neural Tangent Kernel (NTK) for these networks. The analysis explores how the self-adaptive weights influence the eigenvalues of the NTK matrix, equalizing their distribution across different loss components. This equalization helps mitigate imbalances in the training dynamics, which traditionally hinder convergence and accuracy. The NTK analysis suggests that SA-PINNs bring stability and improved convergence properties by reshaping the eigenvalue spectrum, unlike simple scalar weight adjustments.

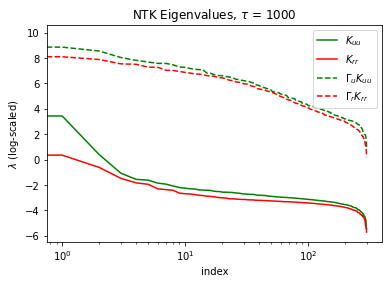
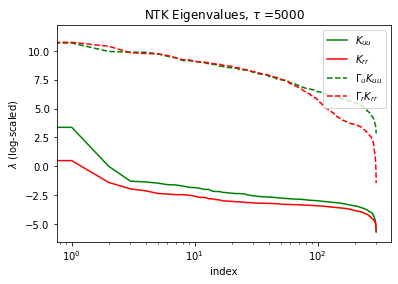
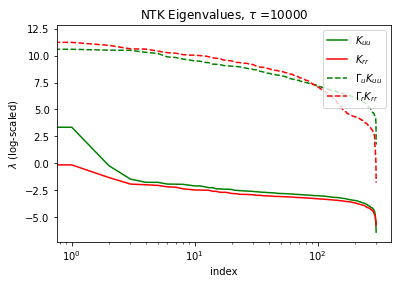
Figure 4: NTK eigenvalues of the baseline PINN (solid) vs. the SA-PINN (dashed) for $\tau=$1000, 5000, and 10000 training iterations.

Conclusion

The introduction of SA-PINNs marks a significant advancement in the numerical solution of PDEs using neural networks. By empowering the network to autonomously identify and focus on challenging areas within the solution space, SA-PINNs offer improved accuracy and efficiency. The theoretical insights provided by the NTK analysis further validate the adaptability and robustness of these networks in handling complex PDEs. Future work could explore refined optimization techniques specifically tailored to SA-PINNs, potentially enhancing their capabilities across a broader range of scientific and engineering applications.