Generalizing Variational Autoencoders with Hierarchical Empirical Bayes (2007.10389v1)

Abstract: Variational Autoencoders (VAEs) have experienced recent success as data-generating models by using simple architectures that do not require significant fine-tuning of hyperparameters. However, VAEs are known to suffer from over-regularization which can lead to failure to escape local maxima. This phenomenon, known as posterior collapse, prevents learning a meaningful latent encoding of the data. Recent methods have mitigated this issue by deterministically moment-matching an aggregated posterior distribution to an aggregate prior. However, abandoning a probabilistic framework (and thus relying on point estimates) can both lead to a discontinuous latent space and generate unrealistic samples. Here we present Hierarchical Empirical Bayes Autoencoder (HEBAE), a computationally stable framework for probabilistic generative models. Our key contributions are two-fold. First, we make gains by placing a hierarchical prior over the encoding distribution, enabling us to adaptively balance the trade-off between minimizing the reconstruction loss function and avoiding over-regularization. Second, we show that assuming a general dependency structure between variables in the latent space produces better convergence onto the mean-field assumption for improved posterior inference. Overall, HEBAE is more robust to a wide-range of hyperparameter initializations than an analogous VAE. Using data from MNIST and CelebA, we illustrate the ability of HEBAE to generate higher quality samples based on FID score than existing autoencoder-based approaches.

• The paper introduces HEBAE, a novel framework that integrates hierarchical empirical Bayes to balance reconstruction and regularization in generative models.
• It employs a Gaussian process prior and non-isotropic posterior assumptions to mitigate over-regularization and avoid posterior collapse.
• Experimental evaluations on MNIST and CelebA demonstrate that HEBAE converges faster and yields higher-quality samples with lower FID scores.

Generalizing Variational Autoencoders with Hierarchical Empirical Bayes

This essay provides a comprehensive analysis of the paper titled "Generalizing Variational Autoencoders with Hierarchical Empirical Bayes," highlighting its contributions to addressing challenges associated with VAEs and WAEs. The Hierarchical Empirical Bayes Autoencoder (HEBAE) is introduced as a novel framework that enhances generative model performance by integrating probabilistic and deterministic elements from VAEs and WAEs.

Background and Motivation

VAEs have been instrumental in generative modeling, facilitating unsupervised learning through structured latent spaces. However, they are susceptible to over-regularization, often resulting in posterior collapse—a scenario where latent representations become uninformative. WAEs, an alternative approach, forsake variational inference in favor of deterministic mappings, yet they fall short in robustness to hyperparameter settings.

The HEBAE framework emerges from a need to balance reconstruction and regularization within a probabilistic generative model, addressing the key limitations inherent in VAEs and WAEs.

HEBAE Framework and Theoretical Contributions

The proposed HEBAE framework introduces a hierarchical prior over the encoding distribution, harmonizing the trade-off between reconstruction loss and over-regularization. It leverages a Gaussian process prior and non-isotropic Gaussian distributions for approximating posteriors, thereby improving the convergence onto standard normal priors.

Key Theoretical Advances:

• Hierarchical Empirical Bayes: By imposing a Gaussian process prior, HEBAE adapts the encoder function to ensure optimal balancing between reconstruction and regularization.
• Non-Isotropic Posterior Assumptions: Allows modeling general covariance structures among latent variables, enhancing posterior distribution matching.
• Regularization Strategy: Employs aggregated posterior regularization similar to WAEs but retains probabilistic inference, mitigating over-regularization and posterior collapse.

  Figure 1: HEBAE outperforms VAE and WAE on all three metrics measured. (a) Top row shows that the ELBO of HEBAE converges faster to a better optimum than VAE in all experiments with different latent dimension $k$. Bottom row shows that HEBAE is less sensitive to different KL divergence weights ($\lambda$) while VAEs are susceptible to over-regularization. Results are based on the MNIST dataset. (b) Comparison of FID scores for HEBAE, VAE, and WAE on the CelebA dataset. HEBAE is less sensitive to $\lambda$ and has the lowest FID score.

Experimental Evaluations

The efficacy of HEBAE is demonstrated through empirical evaluations on the MNIST and CelebA datasets. The framework is assessed against VAEs and WAEs in terms of convergence speed, sensitivity to hyperparameters, and quality of generated samples.

Results:

• ELBO Convergence: HEBAE consistently achieves higher ELBO faster than VAEs across various latent dimensions, indicating efficient optimization with less sensitivity to hyperparameter variations.
• Sample Quality: HEBAE-generated images exhibit lower Fréchet Inception Distances (FID), especially in scenarios demanding robust generative capabilities under varying regularization penalties.

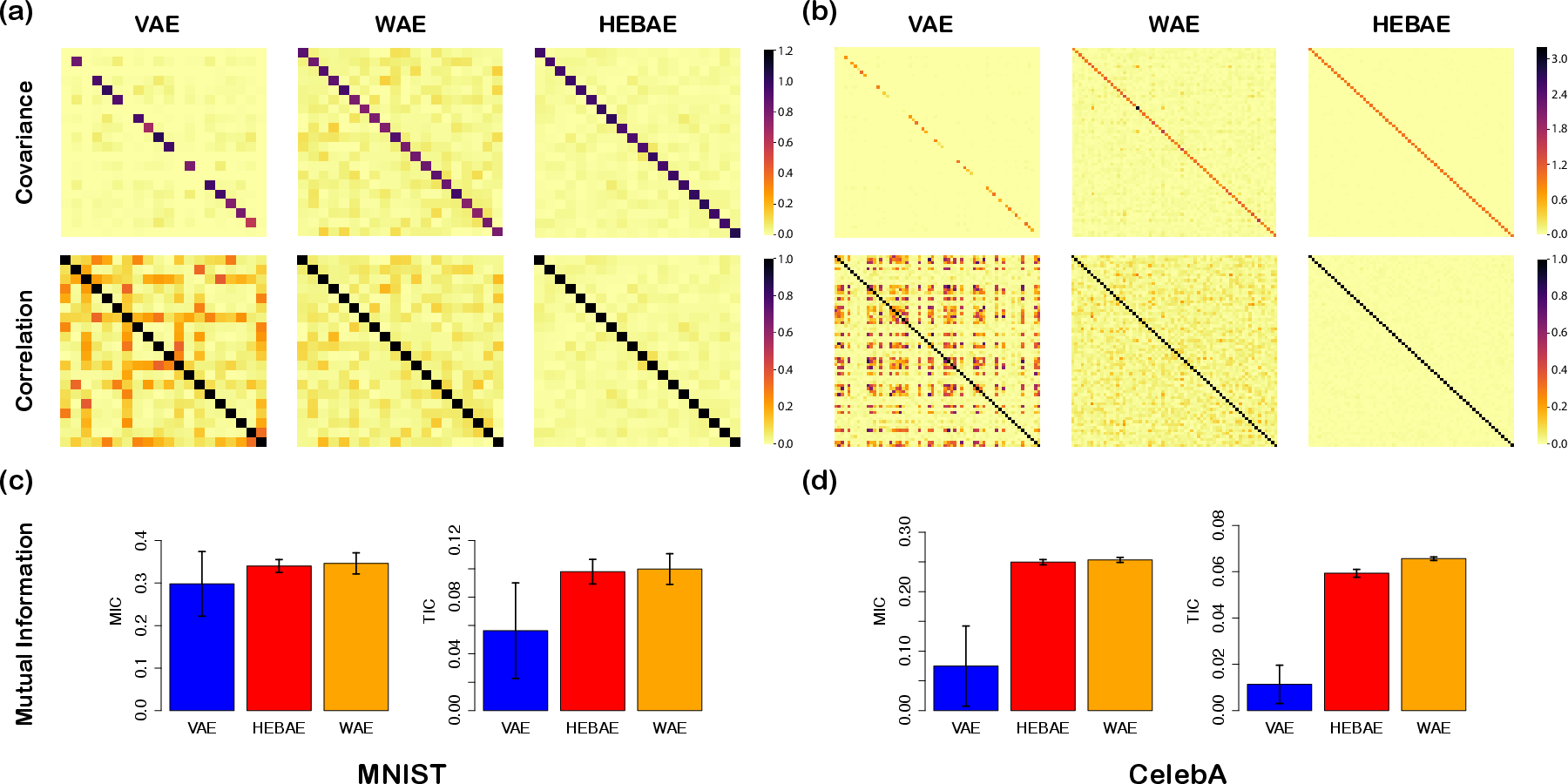
  Figure 2: The estimated posterior of the HEBAE framework is more consistent with the standard normal prior compared to the VAE and WAE frameworks, in both MNIST and CelebA analyses. (a, b) Top row shows the absolute value of the variance-covariance matrices. Bottom row shows the correlation matrices. Results are based on MNIST dataset. (c, d) Averaged mutual information measurements: Maximal Information Coefficient (MIC) and Total Information Coefficient (TIC).

Implications and Future Directions

HEBAE presents substantial improvements in the context of generative models by effectively addressing over-regularization and posterior collapse, critical limitations in VAEs. The integration of probabilistic frameworks with hierarchical assumptions provides a smoother latent space, conducive for higher-quality generative tasks.

Future Research Directions:

• GAN Integration: Potential exists for applying insights from HEBAE to GAN architectures, enhancing their statistical robustness and sample quality.
• Broader Applications: HEBAE could benefit diverse domains such as NLP, robotics, and genomics, where generative models play a pivotal role in developing synthetic data for training and analysis.

  Figure 3: HEBAE produces qualitatively higher-quality images based on the CelebA dataset than the VAE and WAE frameworks. Results on MNIST can be found in the Appendix.

Conclusion

The Hierarchical Empirical Bayes Autoencoder represents an innovative stride in generative modeling, mitigating long-standing VAE challenges while extending theoretical and practical foundations. Its robustness across parameter settings and datasets marks it as a formidable model for future research and application in AI development and beyond. The potential to bridge further into GAN architectures and specialized applications underscores its wide-reaching impact.