Physics-Informed Multi-LSTM Networks for Metamodeling of Nonlinear Structures (2002.10253v1)

Abstract: This paper introduces an innovative physics-informed deep learning framework for metamodeling of nonlinear structural systems with scarce data. The basic concept is to incorporate physics knowledge (e.g., laws of physics, scientific principles) into deep long short-term memory (LSTM) networks, which boosts the learning within a feasible solution space. The physics constraints are embedded in the loss function to enforce the model training which can accurately capture latent system nonlinearity even with very limited available training datasets. Specifically for dynamic structures, physical laws of equation of motion, state dependency and hysteretic constitutive relationship are considered to construct the physics loss. In particular, two physics-informed multi-LSTM network architectures are proposed for structural metamodeling. The satisfactory performance of the proposed framework is successfully demonstrated through two illustrative examples (e.g., nonlinear structures subjected to ground motion excitation). It turns out that the embedded physics can alleviate overfitting issues, reduce the need of big training datasets, and improve the robustness of the trained model for more reliable prediction. As a result, the physics-informed deep learning paradigm outperforms classical non-physics-guided data-driven neural networks.

• The paper introduces physics-informed LSTM architectures (PhyLSTM2 and PhyLSTM3) that embed physical constraints within loss functions for accurate metamodeling of nonlinear structures.
• It leverages multi-LSTM layers to capture latent states like hysteresis, achieving superior accuracy over traditional methods with limited training data.
• Numerical validations on a 3-story steel MRF and a Bouc-Wen model demonstrate enhanced generalizability and robustness in predicting complex structural dynamics.

Physics-Informed Multi-LSTM Networks for Metamodeling of Nonlinear Structures

The paper "Physics-Informed Multi-LSTM Networks for Metamodeling of Nonlinear Structures" introduces a deep learning framework integrating physical laws into LSTM networks for enhanced modeling of nonlinear structures under data constraints. The authors propose physics-informed deep learning techniques, which offer improved generalizability and accuracy over traditional data-driven methods.

Introduction to Physics-Informed Deep Learning

The motivation for employing physics-informed approaches arises from the limitations of computational methods like FEM in handling complex dynamic analyses of large structural systems. The proposed framework embeds physical constraints within LSTM networks, blending data-driven and physics-based modeling. This technique aims to reduce overfitting, improve robustness, and require fewer datasets, thereby addressing challenges associated with purely data-driven models.

In this approach, two multi-LSTM network architectures, PhyLSTM$^2$ and PhyLSTM$^3$, are proposed. These architectures incorporate physical constraints into the loss functions of the LSTM networks, enabling the modeling of latent system dynamics that are often undetectable due to data scarcity.

LSTM Network Architecture

LSTM networks are capable of learning long-term dependencies in sequential data, making them suitable for metamodeling of time-dependent nonlinear systems. The architecture comprises multiple LSTM layers, often followed by fully connected layers, as depicted in the following figure.

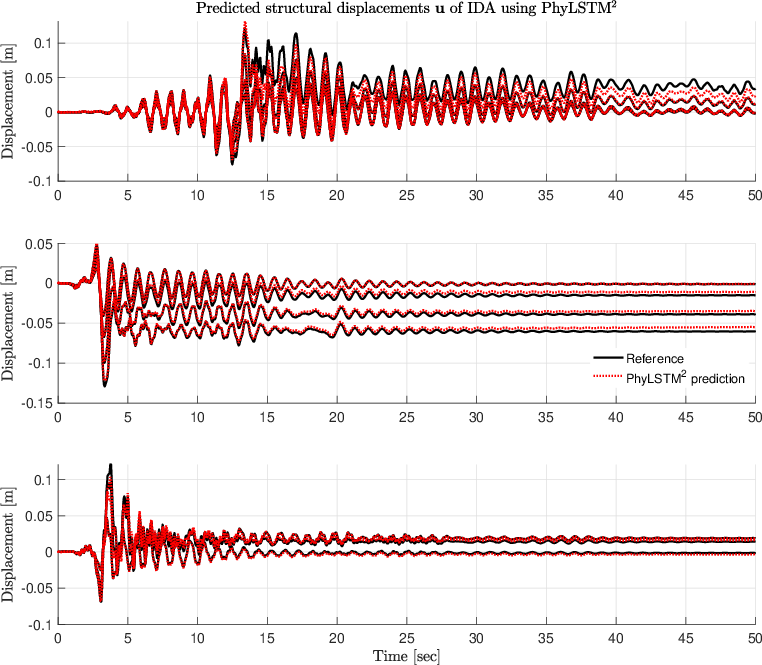
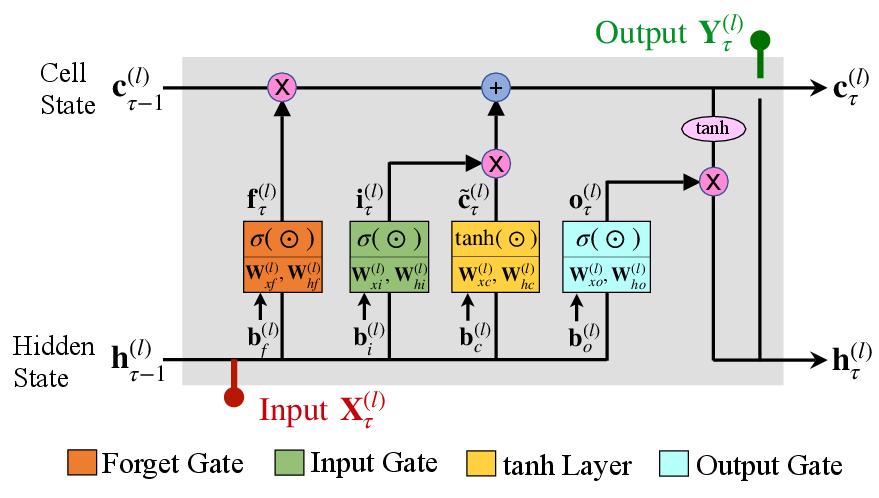
Figure 1: Schematic of deep LSTM networks: (a) architecture of a deep LSTM network with $m$ LSTM layers and multiple fully-connected layers; (b) typical LSTM cell architecture.

Each LSTM cell integrates mechanisms such as input, output, and forget gates, which control the flow and updates of information through the cell, enabling effective sequence modeling.

PhyLSTM$^2$ Architecture

The PhyLSTM$^2$ network consists of two interconnected LSTM networks for capturing state space variables and restoring forces. The physics constraints guide the learning process through additional loss components derived from the equations of motion and state dependencies.

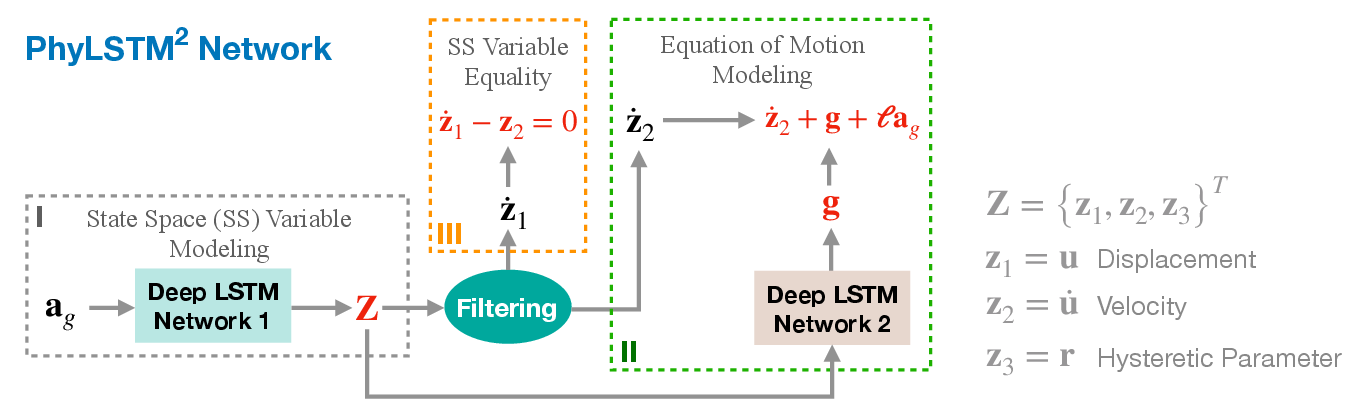
Figure 2: The proposed PhyLSTM$^2$ network architecture.

This architecture effectively models latent structural states like hysteresis parameters, overcoming the need for direct measurements via physics-informative constraints.

PhyLSTM$^3$ Architecture

For systems with complex rate-dependent hysteresis, PhyLSTM$^3$ extends the capability of PhyLSTM$^2$ by introducing a third LSTM network to model additional hysteretic behaviors.

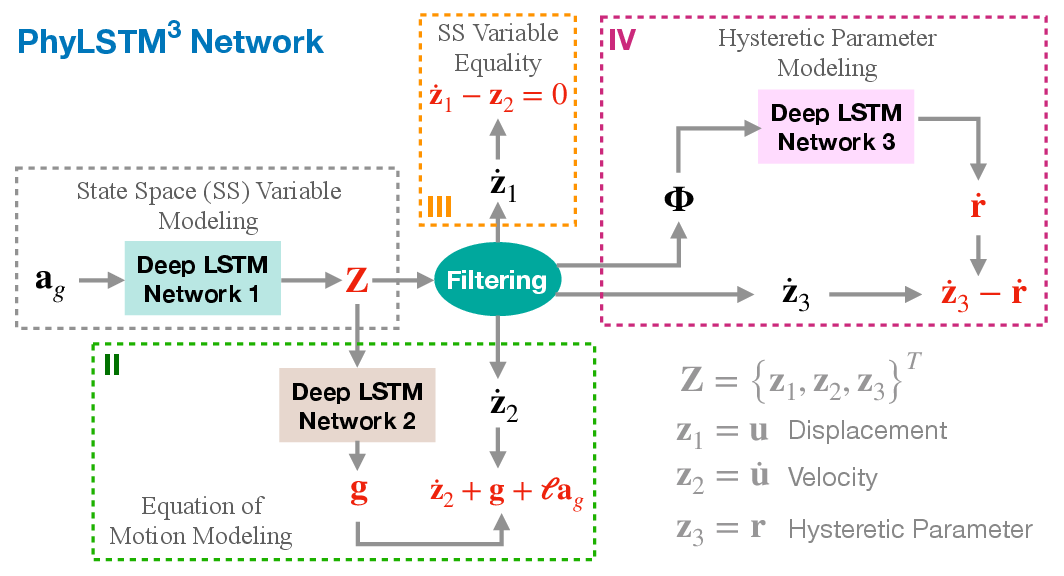
Figure 3: The proposed PhyLSTM$^3$ network architecture.

This architecture's versatility is demonstrated in modeling nonlinear behaviors where conventional methods may falter, showcasing its superior predictive abilities in complex dynamical systems.

Numerical Validation

The effectiveness of the proposed models is validated through two numerical examples: a 3-story steel moment-resisting frame (MRF) and a Bouc-Wen hysteresis model. In both cases, PhyLSTM approaches significantly outperform traditional LSTM, providing more accurate predictions even with limited training data.

Steel MRF Structure

The architecture's adaptability to model nonlinear seismic responses is illustrated through regression analyses and predicted time histories.

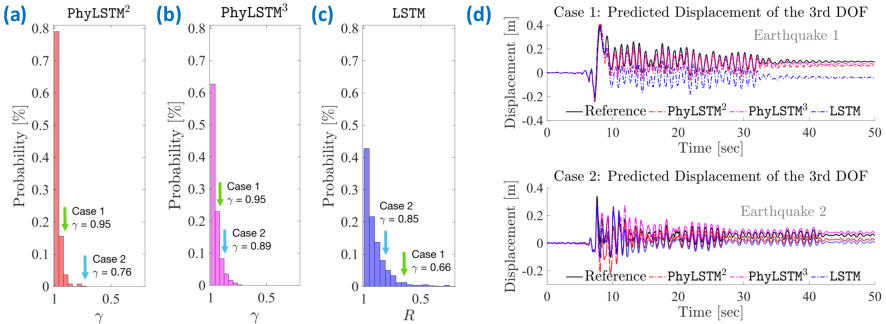
Figure 4: Performance of PhyLSTM$^2$ and PhyLSTM$^3$ for nonlinear displacement prediction.

Bouc-Wen Hysteresis Model

For the Bouc-Wen model, PhyLSTM$^3$ delivers precise predictions of nonlinear dynamics and hysteretic behaviors, highlighting its robustness.

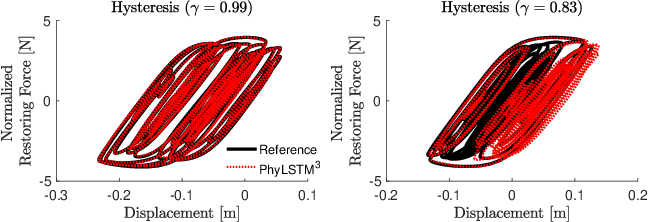
Figure 5: Predicted hysteresis curves using PhyLSTM$^3$.

Conclusion

The paper demonstrates that embedding physical constraints within LSTM networks fosters potent metamodels for nonlinear structures, excelling over traditional methods. These physics-informed architectures provide interpretable, reliable, and generalizable predictions, showcasing substantial potential for application in diverse engineering problems.

Future advancements can explore expanded applications beyond structural seismic response, such as other domains of complex dynamic systems modeling, harnessing the strengths of integrated data-physics paradigms.