A Diffusion Theory For Deep Learning Dynamics: Stochastic Gradient Descent Exponentially Favors Flat Minima (2002.03495v14)

Abstract: Stochastic Gradient Descent (SGD) and its variants are mainstream methods for training deep networks in practice. SGD is known to find a flat minimum that often generalizes well. However, it is mathematically unclear how deep learning can select a flat minimum among so many minima. To answer the question quantitatively, we develop a density diffusion theory (DDT) to reveal how minima selection quantitatively depends on the minima sharpness and the hyperparameters. To the best of our knowledge, we are the first to theoretically and empirically prove that, benefited from the Hessian-dependent covariance of stochastic gradient noise, SGD favors flat minima exponentially more than sharp minima, while Gradient Descent (GD) with injected white noise favors flat minima only polynomially more than sharp minima. We also reveal that either a small learning rate or large-batch training requires exponentially many iterations to escape from minima in terms of the ratio of the batch size and learning rate. Thus, large-batch training cannot search flat minima efficiently in a realistic computational time.

• The paper develops a diffusion theory that quantitatively links SGD’s anisotropic gradient noise to its exponential preference for flat minima.
• It demonstrates that the covariance of the gradient noise aligns with the loss Hessian, influencing escape dynamics from sharp minima.
• Empirical results confirm that hyperparameters like batch size and learning rate critically impact SGD dynamics and minima selection.

A Diffusion Theory For Deep Learning Dynamics: Stochastic Gradient Descent Exponentially Favors Flat Minima

Overview

The paper "A Diffusion Theory For Deep Learning Dynamics: Stochastic Gradient Descent Exponentially Favors Flat Minima" focuses on the understanding of how Stochastic Gradient Descent (SGD) biases towards selecting flat minima over sharp minima in the loss landscape during the training of deep neural networks. This is achieved through the development of a novel density diffusion theory (DDT). The authors provide theoretical and empirical evidence that SGD's stochastic gradient noise (SGN), which is parameter-dependent and anisotropic, plays a crucial role in this selection process.

Contributions

The paper makes several key contributions to the understanding of deep learning dynamics:

1. Diffusion Theory Development: A theoretical framework is established that quantitatively relates the selection of flat minima to hyperparameters such as batch size, learning rate, and gradient noise characteristics. This framework bridges the gap between existing qualitative observations and quantitative theories.
2. SGN Structure: It is demonstrated that the covariance of SGN is approximately proportional to the Hessian of the loss at critical points and inversely proportional to the batch size. This insight challenges previous assumptions of isotropic and parameter-independent noise.
3. Theoretical Insights: The paper provides a novel explanation for why large-batch and small learning rate training might require exponentially more iterations to escape sharp minima, leading to less effective search of the parameter space.
4. Minima Selection: It is theoretically and empirically shown that SGD favors flat minima exponentially more than sharp minima, contrasting with the polynomial favoring seen in approaches like Gradient Descent (GD) with injected white noise.

Stochastic Gradient Noise and Its Role

In training settings, SGN arises from the use of minibatches and is modeled by a Gaussian distribution, albeit with parameter-dependent covariance. The paper supports this claim with empirical evidence that counters previous findings suggesting heavy-tailed distributions.

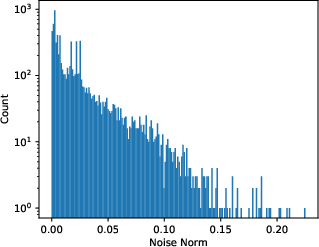
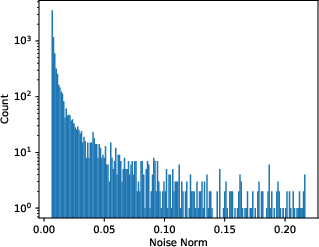
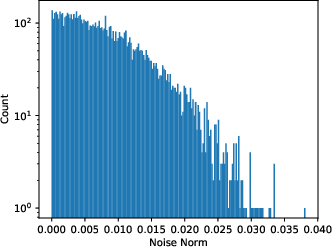
Figure 1: The Stochastic Gradient Noise Analysis showing similarity to Gaussian noise as computed with a fully connected network on MNIST.

The covariance structure of SGN is derived to be closely tied to the Hessian, explaining why SGD dynamics are sensitive to the curvature of the loss landscape.

Theoretical Framework for SGD Dynamics

The authors develop the density diffusion theory for SGD starting from classical Kramers escape problems. In statistical mechanics, this relates to understanding how systems escape local minima through stochastic processes.

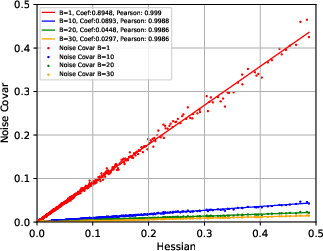
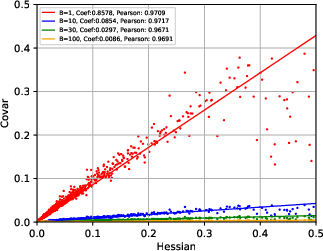
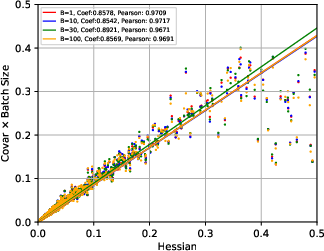
Figure 2: Escape dynamics in high-dimensional SGD configurations highlighting path Hessians as key factors.

A critical finding is that the mean escape time from a sharp to a flat minimum is exponentially dependent on the path Hessian's eigenvalues. This result explains the empirical success of SGD in finding solutions that generalize well due to their location in flatter regions of the loss surface.

Empirical Validation

Extensive experiments across datasets and model architectures validate the theoretical predictions. The experiments demonstrate how the escape rate from loss valleys depends exponentially on parameters like the path Hessian, batch size, and learning rate.

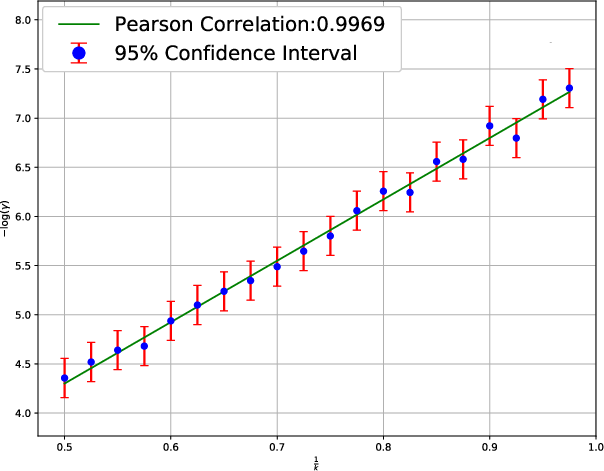
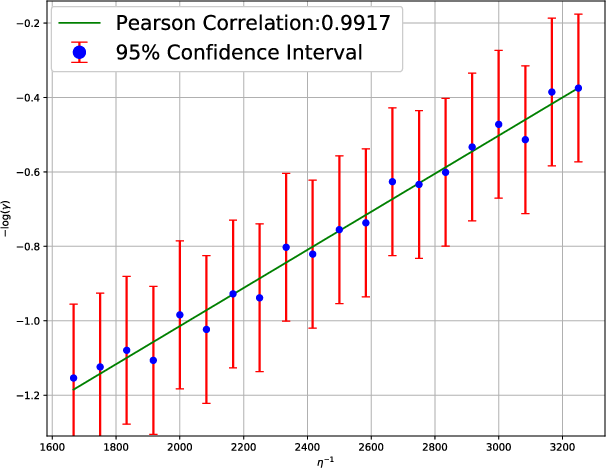
Figure 3: The mean escape time analysis by using the Styblinski-Tang Function, evidencing the dependence on learning dynamics.

These empirical studies reinforce the core propositions of the paper that large-batch training requires a careful balance of hyperparameters to maintain effective minima exploration.

Implications and Future Directions

The findings have significant implications for the optimization strategies employed in deep learning. Understanding the dynamics by which SGD selects solutions can guide the design of new training regimes that favor better generalization. The insights about the exponential effects of batch size and learning rate on training dynamics can also impact how practitioners choose these parameters in practice.

Future research may involve expanding the diffusion theory to incorporate higher-order effects and exploring scenarios where third-order dynamics become significant.

Conclusion

The paper provides a comprehensive and quantitative understanding of why SGD effectively finds flat minima and how different factors influence its dynamics. It lays a foundation for future work to explore anisotropic noise behaviors more deeply and to refine optimization techniques for deep learning.