High-Dimensional Multivariate Forecasting with Low-Rank Gaussian Copula Processes (1910.03002v2)

Abstract: Predicting the dependencies between observations from multiple time series is critical for applications such as anomaly detection, financial risk management, causal analysis, or demand forecasting. However, the computational and numerical difficulties of estimating time-varying and high-dimensional covariance matrices often limits existing methods to handling at most a few hundred dimensions or requires making strong assumptions on the dependence between series. We propose to combine an RNN-based time series model with a Gaussian copula process output model with a low-rank covariance structure to reduce the computational complexity and handle non-Gaussian marginal distributions. This permits to drastically reduce the number of parameters and consequently allows the modeling of time-varying correlations of thousands of time series. We show on several real-world datasets that our method provides significant accuracy improvements over state-of-the-art baselines and perform an ablation study analyzing the contributions of the different components of our model.

• The paper proposes a novel forecasting approach combining an LSTM-based RNN with a low-rank Gaussian copula process to model high-dimensional time series.
• It employs marginal transformations and a low-rank covariance parametrization to efficiently capture time-varying correlations and complex non-Gaussian distributions.
• Empirical results show improved performance, achieving up to 10% and 40% gains in CRPS and CRPS-Sum compared to state-of-the-art baselines.

High-Dimensional Time Series Forecasting with Gaussian Copula Processes

This paper introduces a novel approach for high-dimensional multivariate time series forecasting by combining an RNN-based model with a low-rank Gaussian copula process. The method addresses the computational challenges associated with estimating high-dimensional covariance matrices and modeling non-Gaussian marginal distributions, enabling the modeling of time-varying correlations across thousands of time series. The authors demonstrate significant accuracy improvements over state-of-the-art baselines on several real-world datasets.

Model Architecture

The proposed model leverages an autoregressive RNN to capture temporal dependencies in individual time series, combined with a Gaussian copula process to model the joint emission distribution (Figure 1).

Figure 1: Illustration of the model parametrization, highlighting the random sampling of dimensions during training and the shared parameters across time series.

Specifically, the model consists of the following components:

• RNN-based State Space Model: An LSTM-RNN is used to model the temporal evolution of each individual time series. The LSTM is unrolled independently for each series, but the parameters are tied across all series. The hidden state $h_{i,t}$ for each time series $i$ at time $t$ is updated based on the previous state and the previous observation $z_{i, t-1}$.

  $$h_{i, t} = \varphi_{\theta_h}(h_{i, t-1}, z_{i, t-1})$$

• Marginal Transformation with Empirical CDF: To handle different scales and non-Gaussian data, each time series' marginal distribution is modeled separately using a non-parametric estimate of its CDF, $\hat{F}_i$. This CDF estimate is then used as the marginal transformation in a Gaussian copula, effectively decoupling the estimation of marginal distributions from the temporal dynamics and dependency structure. The transformation $f_i: \mathcal{D} \rightarrow \mathbb{R}$ is defined as $f_i = \Phi^{-1} \circ \hat{F}_i$, where $\Phi$ is the CDF of the standard normal distribution.
• Gaussian Copula Process: A Gaussian copula is used to model the joint distribution of the transformed observations. The copula is parametrized by a mean vector $(h_t)$ and a covariance matrix $\Sigma(h_t)$, both of which are functions of the LSTM states $h_t$.

  $$p(z_{t}|h_{t}) = \mathcal{N}(\left[f_1(z_{1, t}), f_2(z_{2, t}), \ldots, f_N(z_{N, t})\right]^T |~ (h_t), \Sigma(h_t)).$$

• Low-Rank Covariance Structure: To reduce the computational complexity and the number of parameters, the covariance matrix $\Sigma(h_t)$ is parametrized as the sum of a diagonal matrix $D_t$ and a low-rank matrix $V_t V_t^T$, where $V_t \in \mathbb{R}^{N \times r}$ and $r \ll N$. This parametrization allows the likelihood to be evaluated using $O(Nr^2 + r^3)$ operations instead of $O(N^3)$.

  $\Sigma(h_t) = D_t + V_t V_t^T$

Implementation Details

The model is trained by minimizing the negative log-likelihood of the observed data using stochastic gradient descent. To handle long time series, a data augmentation strategy is employed where fixed-size slices of the time series are randomly sampled during training. The parameters of the LSTM, the mean and covariance mappings are learned jointly from the data.

The authors also propose a Gaussian Process (GP) interpretation of the model, where the distribution of the transformed data $x_t$ is viewed as a GP evaluated at points $y_{i, t} = [h_{i, t}; e_i]^T$. This GP perspective enables training the model on random subsets of the time series in each iteration, further alleviating memory constraints and allowing the model to be applied to very high-dimensional datasets.

Experimental Results

The proposed method was evaluated on several real-world datasets, including exchange rates, solar power production, electricity consumption, traffic occupancy rates, taxi demand, and Wikipedia page views. The results demonstrate that the proposed model achieves significant accuracy improvements over state-of-the-art baselines, including VAR, GARCH, and various LSTM architectures.

The authors also present a synthetic experiment to demonstrate that the model can recover complex time-varying low-rank covariance patterns from multi-dimensional observations (Figure 2).

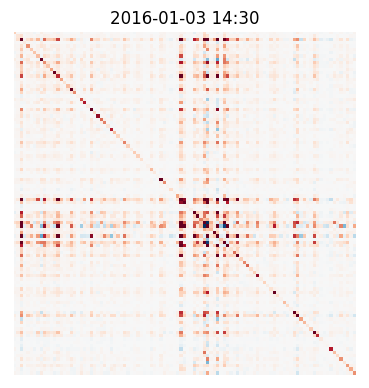
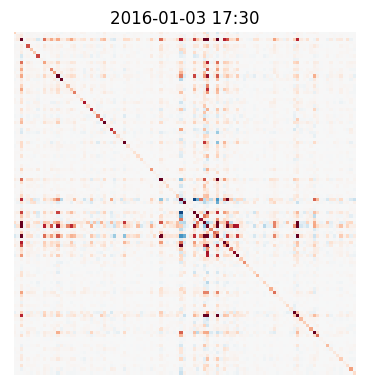
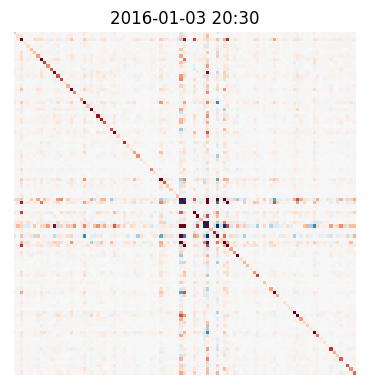
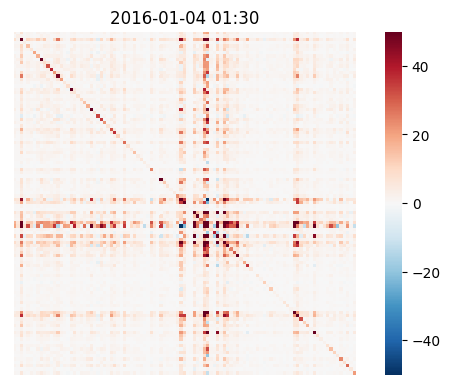
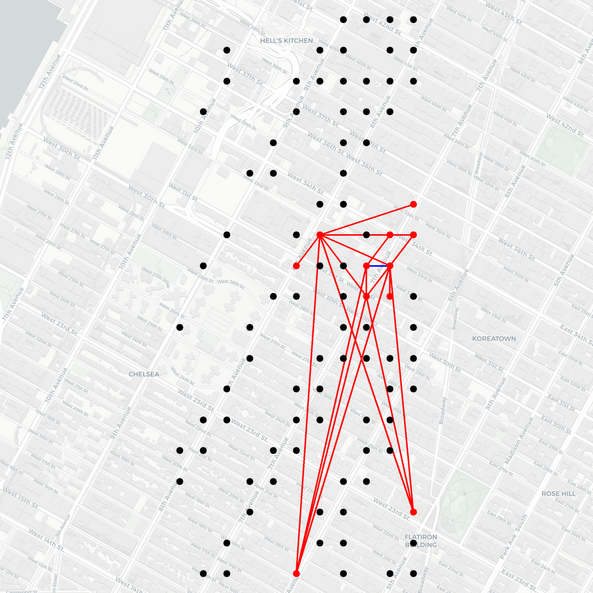
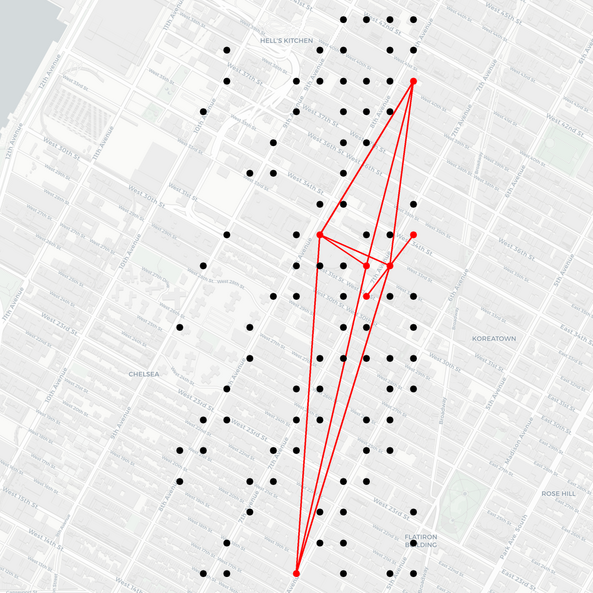
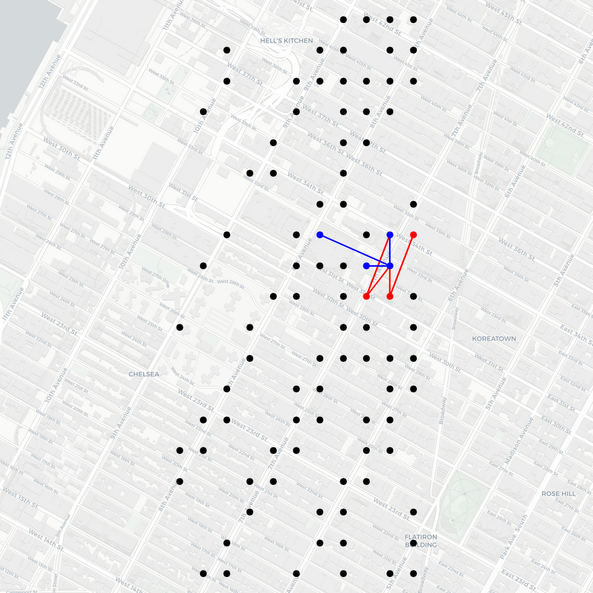
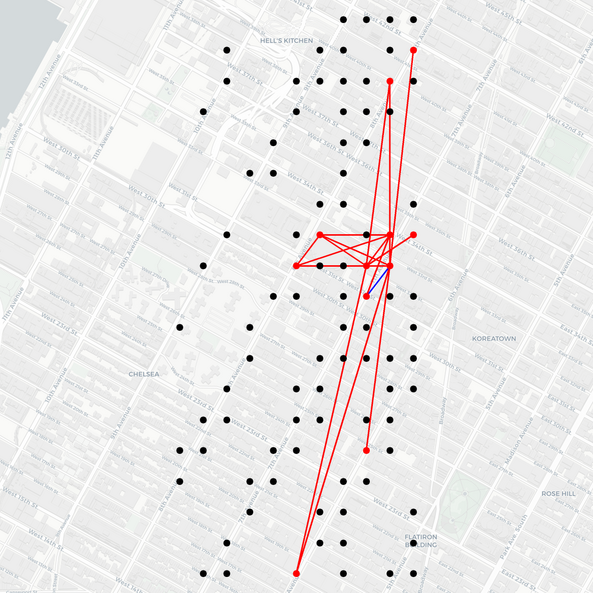
Figure 2: Comparison of true and predicted covariance matrices after training on synthetic data, showing the model's ability to capture complex covariance patterns.

Specifically, the GP-Copula model improves CRPS and CRPS-Sum by 10% and 40% respectively, compared to the second best models. Furthermore, the proposed model achieves these improvements with a significantly smaller number of parameters compared to other deep learning-based approaches.

Conclusion

The paper presents a method for probabilistic forecasting of high-dimensional multivariate time series using a low-rank Gaussian copula process. The proposed approach addresses the computational challenges associated with high-dimensional covariance estimation and non-Gaussian data, and achieves significant accuracy improvements over state-of-the-art baselines. The authors suggest that the ability to estimate high-dimensional time-varying covariance matrices could enable several applications in anomaly detection, imputation, and graph analysis for time series data.