Stochastic gradient Markov chain Monte Carlo (1907.06986v1)

Abstract: Markov chain Monte Carlo (MCMC) algorithms are generally regarded as the gold standard technique for Bayesian inference. They are theoretically well-understood and conceptually simple to apply in practice. The drawback of MCMC is that in general performing exact inference requires all of the data to be processed at each iteration of the algorithm. For large data sets, the computational cost of MCMC can be prohibitive, which has led to recent developments in scalable Monte Carlo algorithms that have a significantly lower computational cost than standard MCMC. In this paper, we focus on a particular class of scalable Monte Carlo algorithms, stochastic gradient Markov chain Monte Carlo (SGMCMC) which utilises data subsampling techniques to reduce the per-iteration cost of MCMC. We provide an introduction to some popular SGMCMC algorithms and review the supporting theoretical results, as well as comparing the efficiency of SGMCMC algorithms against MCMC on benchmark examples. The supporting R code is available online.

• The paper presents a scalable SGMCMC framework that applies Langevin dynamics with subsampled gradients to reduce computational costs.
• The method extends to advanced schemes like SG-HMC, integrating auxiliary variables and Riemannian adjustments for efficient high-dimensional exploration.
• The paper highlights diagnostic techniques such as Kernel Stein Discrepancy to effectively tune parameters and balance bias and variance.

Stochastic Gradient Markov Chain Monte Carlo

Introduction

The "Stochastic Gradient Markov Chain Monte Carlo" paper presents a class of scalable Monte Carlo algorithms designed for Bayesian inference in large datasets. Traditional MCMC methods, while robust and theoretically sound, struggle with computational costs in big data contexts as they require full data sweeps every iteration. SGMCMC addresses this by employing data subsampling to significantly reduce such costs, thus making MCMC feasible on large-scale problems.

Langevin-based Stochastic Gradient MCMC

The core of SGMCMC draws from the Langevin dynamics, a stochastic process known for its applications in sampling from a target density $\pi()$. The Langevin diffusion is expressed through a stochastic differential equation (SDE), which is then discretized to form the basics of SGMCMC methods. A typical example is the Stochastic Gradient Langevin Dynamics (SGLD), which introduces unbiased gradient estimation through data subsampling, replacing the full gradient seen in traditional methods. This substitution brings a substantial reduction in per-iteration computational demands. However, this method induces bias, and thus careful tuning of the step size parameter becomes crucial for effectiveness.

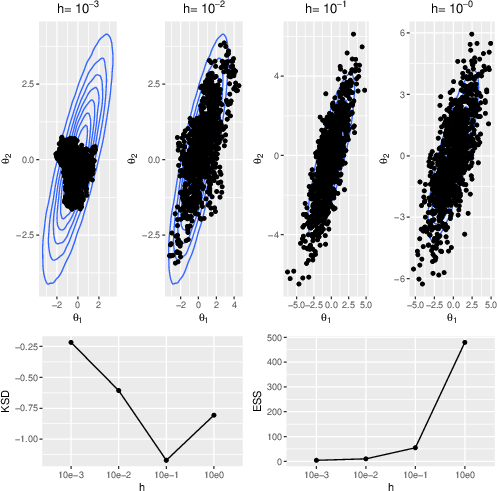
Figure 1: Top: Samples generated from the Langevin dynamics $eq:gaussian-example-dynamics$.

Advanced SGMCMC Frameworks

The paper extends the SGMCMC framework beyond basic Langevin dynamics to include a broader range of stochastic processes. This includes the integration of auxiliary variables and various algorithmic structures such as Riemannian manifold adjustments, which improve adaptation to local structures of the target distribution. For instance, the Stochastic Gradient Hamiltonian Monte Carlo (SG-HMC) exploits auxiliary momentum variables to enhance convergence in high-dimensional spaces. These extensions demonstrate the flexibility and generalizability of the SGMCMC framework, allowing for more efficient exploration of complex posterior distributions.

Diagnostic and Tuning Considerations

Proper tuning and diagnostics are central to the successful application of SGMCMC methods. Traditional MCMC diagnostics like effective sample size and trace plots are not directly applicable due to the inherent bias introduced by subsampling techniques. Instead, the Kernel Stein Discrepancy (KSD), a measure of how well a Markov chain has converged, is advocated. This metric is pivotal in tuning parameters such as step size to balance bias and variance effectively.

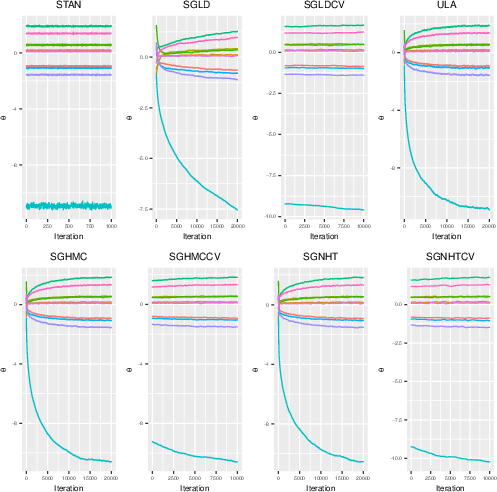
Figure 2: Trace plots for the STAN output and each SGMCMC algorithm with $d=10$ and $N=10^5$.

Applications and Performance

SGMCMC's applicability is demonstrated across various models, including logistic regression, Bayesian neural networks, and probabilistic matrix factorization models. In these domains, SGMCMC algorithms were compared with traditional MCMC algorithms like those implemented in STAN. The results consistently show competitive performance with significant computational savings, especially in high-dimensional parameter spaces. SGMCMC methods leveraged control variates for variance reduction, further enhancing their efficiency.

Figure 3: Sample of images from the MNIST data set taken from \url{https://en.wikipedia.org/wiki/MNIST\_database.}

Conclusions and Future Work

The SGMCMC paper showcases these methods as powerful tools for scalable Bayesian inference, particularly suitable for large datasets. Their development opens avenues for future work in algorithmic innovation, theoretical extensions beyond log-concave distributions, and the creation of robust, user-friendly software tools. These advancements will help broaden SGMCMC's applicability and ease of use across diverse fields requiring complex data analysis.

The continued progress in this space is anticipated to support further breakthroughs in fields demanding scalable, efficient, and reliable statistical computation. The paper serves as a critical step in that direction, underlining SGMCMC's potential to redefine the capabilities of Monte Carlo methods in the era of big data.