The Shapley Taylor Interaction Index (1902.05622v2)

Abstract: The attribution problem, that is the problem of attributing a model's prediction to its base features, is well-studied. We extend the notion of attribution to also apply to feature interactions. The Shapley value is a commonly used method to attribute a model's prediction to its base features. We propose a generalization of the Shapley value called Shapley-Taylor index that attributes the model's prediction to interactions of subsets of features up to some size k. The method is analogous to how the truncated Taylor Series decomposes the function value at a certain point using its derivatives at a different point. In fact, we show that the Shapley Taylor index is equal to the Taylor Series of the multilinear extension of the set-theoretic behavior of the model. We axiomatize this method using the standard Shapley axioms -- linearity, dummy, symmetry and efficiency -- and an additional axiom that we call the interaction distribution axiom. This new axiom explicitly characterizes how interactions are distributed for a class of functions that model pure interaction. We contrast the Shapley-Taylor index against the previously proposed Shapley Interaction index (cf. [9]) from the cooperative game theory literature. We also apply the Shapley Taylor index to three models and identify interesting qualitative insights.

• The paper introduces the Shapley-Taylor index, extending traditional Shapley values to measure both individual contributions and feature interactions via a Taylor series approach.
• It establishes a rigorous axiomatic foundation with five principles, including the novel interaction distribution axiom, ensuring balanced attribution.
• Practical applications in sentiment analysis, random forest regression, and reading comprehension highlight its ability to uncover nuanced feature interactions.

The Shapley-Taylor Interaction Index

Introduction

The paper "The Shapley Taylor Interaction Index" (1902.05622) extends the Shapley value attribution method to quantify feature interactions in machine learning models. This extension, known as the Shapley-Taylor index, attributes predictions not only to individual features but also to interactions between feature subsets, resembling the Taylor series' decomposition approach. The authors axiomatize this method using standard Shapley assumptions alongside a new one called the interaction distribution axiom. This paper provides both theoretical foundations and practical applications of the Shapley-Taylor index, comparing it with existing methods, such as the Shapley Interaction index from cooperative game theory.

Shapley-Taylor Index Definition

The Shapley value traditionally assigns a model's prediction to its basic features, distributing contributions over various possible feature orderings. The Shapley-Taylor index generalizes this by also considering feature interactions up to a chosen size $k$. For an input with feature set $N$, the Shapley-Taylor index is computed using the derivative-like expressions $\delta_S F(T)$ for subsets $S$ of $N$. This is analogous to taking higher-order derivatives in Taylor series expansions, capturing the effect of feature interactions. The interaction indices are computed by considering permutations of features, similarly to the standard Shapley value setup.

Axiomatic Foundation

The Shapley-Taylor index is axiomatized using five key principles:

1. Linearity: The index should be a linear transformation of the input model.
2. Dummy Axiom: If a feature does not contribute to any interaction, its index is zero.
3. Symmetry: Identical features should receive identical attributions under feature permutation.
4. Efficiency: The sum of attributions should equal the model's prediction minus its baseline score.
5. Interaction Distribution Axiom: Higher-order interactions should only be captured by indices of sufficient order and not be misattributed to lower-order indices.

These axioms ensure that the Shapley-Taylor index properly attributes both independent feature effects and their interactions.

Comparison with Shapley Interaction Index

The paper contrasts the Shapley-Taylor index with Shapley Interaction indices. Shapley's Interaction indices, which also aim to capture feature interactions, do not satisfy the efficiency axiom leading to inflated interaction terms. This inflation happens because Shapley Interaction indices focus solely on interactions without the condition that the sum of all interaction values matches the total model output. The Shapley-Taylor indices, by enforcing efficiency, provide a more balanced interaction measurement that aligns with the theory of cooperative games.

Application and Insights

The Shapley-Taylor index is applied to real-world tasks to uncover interesting feature interactions:

• Sentiment Analysis: The method reveals interactions such as negation (e.g., "not good"), emphasizing how the Shapley-Taylor index captures context-level nuances in text data.
• Random Forest Regression: For this task, the major interactions identified are substitutes, which often occurs due to the correlation of features, as demonstrated in Figure 1.
• Reading Comprehension: Using the QANet model on the SQuAD dataset, the index highlights word matches between questions and text that are crucial for deriving context-based answers, as shown in Figure 2.

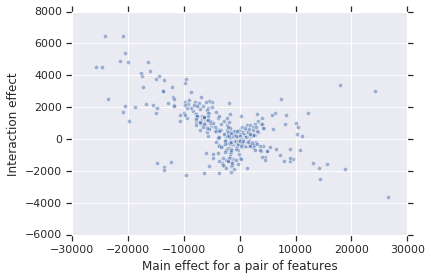
Figure 1: A plot of main effects of pairs of features vs interaction effect for the pair. Negative slope indicates substitutes.

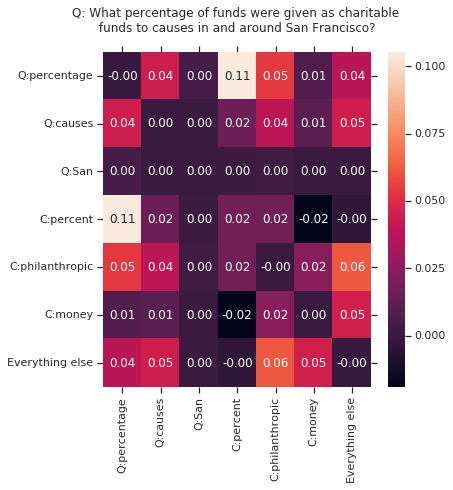
Figure 2: First example shows a match between percentage in question to percent in the context. Second example shows total touchdowns matching between the question and the context.

Conclusion

The Shapley-Taylor Interaction Index offers a significant advancement in model interpretation by identifying and quantifying feature interactions. By addressing feature interactions up to a certain order, this index provides richer insights than traditional attribution methods. The axiomatic approach solidifies its theoretical foundation and practical applications demonstrate its utility in real-world scenarios. By comparing Shapley-Taylor indices with previous methods, this paper contributes a valuable tool for understanding complex interactions in sophisticated models like deep networks.