MetaBags: Bagged Meta-Decision Trees for Regression (1804.06207v1)

Abstract: Ensembles are popular methods for solving practical supervised learning problems. They reduce the risk of having underperforming models in production-grade software. Although critical, methods for learning heterogeneous regression ensembles have not been proposed at large scale, whereas in classical ML literature, stacking, cascading and voting are mostly restricted to classification problems. Regression poses distinct learning challenges that may result in poor performance, even when using well established homogeneous ensemble schemas such as bagging or boosting. In this paper, we introduce MetaBags, a novel, practically useful stacking framework for regression. MetaBags is a meta-learning algorithm that learns a set of meta-decision trees designed to select one base model (i.e. expert) for each query, and focuses on inductive bias reduction. A set of meta-decision trees are learned using different types of meta-features, specially created for this purpose - to then be bagged at meta-level. This procedure is designed to learn a model with a fair bias-variance trade-off, and its improvement over base model performance is correlated with the prediction diversity of different experts on specific input space subregions. The proposed method and meta-features are designed in such a way that they enable good predictive performance even in subregions of space which are not adequately represented in the available training data. An exhaustive empirical testing of the method was performed, evaluating both generalization error and scalability of the approach on synthetic, open and real-world application datasets. The obtained results show that our method significantly outperforms existing state-of-the-art approaches.

• The paper introduces a novel meta-learning framework that uses bagged meta-decision trees to dynamically select base regression models.
• It employs a unique Maximum Bias Reduction impurity function which guides tree splits for improved expert selection and generalization.
• Empirical evaluations on diverse datasets demonstrate that MetaBags outperforms state-of-the-art stacking methods while scaling efficiently.

MetaBags: Bagged Meta-Decision Trees for Regression

The paper introduces MetaBags, a novel meta-learning framework for regression that utilizes bagged meta-decision trees to select base models (experts) for each query, with the goal of reducing inductive bias. The approach involves learning a set of meta-decision trees on different bootstrap samples, using meta-features to select suitable base models, and aggregating their predictions. Empirical results demonstrate that MetaBags outperforms existing state-of-the-art approaches in terms of generalization error and scalability.

Key Components and Implementation Details

MetaBags consists of three main components: meta-decision tree learning, meta-level bagging, and meta-feature generation. (Figure 1) provides an overview of the MetaBags framework.

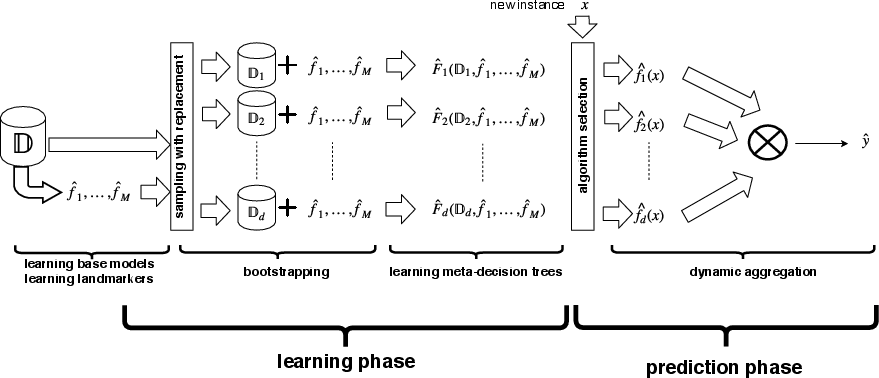
Figure 1: MetaBags: the learning/induction and prediction phases.

Meta-Decision Tree Learning

The meta-decision tree aims to dynamically select the most appropriate expert for a given query by constructing a classification tree. Unlike traditional decision trees that minimize the entropy of the target variable, MetaBags employs a novel impurity function called Maximum Bias Reduction (MBR). The MBR function, defined in Equation 3 of the paper, seeks to maximize the reduction of inductive bias, $B(\mathcal{L})$, of the loss $\mathcal{L}$. The tree induction process involves finding the feature $z_j$ and splitting point $z_j^t$ that maximize impurity reduction at each node. The optimization problem, formulated in Equations 4 and 5, is solved by constructing auxiliary matrices and using a simplified Golden-section search algorithm to find the optimal splitting point. The stopping criterion for tree growth is based on a minimum bias reduction threshold $\epsilon$ and a minimum number of examples per node $\upsilon$. The pseudocode for the algorithm is presented as Algorithm 1 in the paper.

Bagging at the Meta-Level

MetaBags employs bagging to enhance the stability and generalization performance of the meta-decision trees. By creating multiple bootstrap datasets $\mathbb{D}^{(B)}$ and learning a meta-decision tree on each, the approach aims to reduce overfitting and improve prediction accuracy. The expected improvement of the aggregated prediction $\varphi_A(x_i)$ depends on the inequality in Equation 7. The instability of $\varphi$, caused by the selection of different predictors by each tree, is leveraged to improve overall performance, especially when the dominant regions of each expert are equally sized.

Meta-Feature Generation

MetaBags utilizes three types of meta-features: base features, performance-related features, and local landmarking features.

1. Base Features: The inclusion of all base features as meta-features aims to increase the inductive variance of individual meta-predictors.
2. Performance-Related Features: These features describe the performance of specific learning algorithms in particular learning contexts, including landmarkers such as LASSO, 1NN, MARS, and CART. Landmarking models are created for each method, and a small artificial neighborhood of size $\psi$ is generated around each training example $x_i$. Descriptive statistics of the models' outputs are then used as meta-features.
3. Local Landmarking Features: These novel meta-features characterize the landmarkers/models within specific input subregions. They aim to extract knowledge learned by the landmarkers about a particular input neighborhood, including CART leaf depth and example variance, MARS interval width, mass, and distance to the nearest edge, and 1NN absolute distance to the nearest neighbor.

Experimental Evaluation and Results

The empirical evaluation addresses four key research questions related to the performance, scalability, and impact of local landmarking features of MetaBags. The experiments were conducted on 17 benchmark datasets and 4 proprietary datasets related to public transportation travel time prediction. The evaluation methodology involved 5-fold cross-validation with 3 repetitions, and comparison against several algorithms, including SVR, PPR, RF, GB, Linear Stacking (LS), and Dynamic Selection (DS). Hyperparameters were tuned using random search and 3-fold cross-validation.

The results, summarized in Table 3, demonstrate that MetaBags outperforms existing state-of-the-art stacking methods and is never statistically significantly worse than any other method. (Figure 2) summarizes these results, highlighting the contributions of bagging at the meta-level and the local landmarking meta-features.

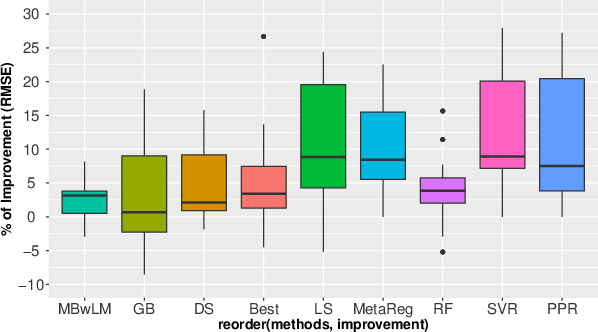
Figure 2: Summary results of MetaBags using the percentage of improvement over its competitors. Note the consistently positive mean over all methods.

(Figure 3) depicts the scalability of MetaBags.

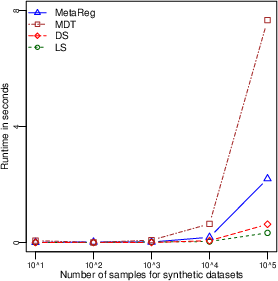
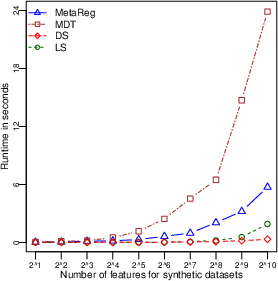
Figure 3: Empirical runtime scalability analysis of MetaBags resorting to samples (left panel) and features (right panel) size. Times in seconds.

Discussion and Future Work

The empirical results indicate that MetaBags effectively addresses model integration problems in regression. The introduction of bagging at the meta-level and the novel local landmarking meta-features contribute to improved performance. While MetaBags demonstrates competitive scalability, its space complexity and the computational cost of meta-feature calculation may pose challenges for low-latency applications. Future research directions include investigating factors affecting MetaBags performance at the model generation level and addressing its time and spatial complexity in test time. Formal approaches to ensure diversity in model generation for ensemble learning in regression also remain an open research question.

Conclusion

MetaBags offers a practical stacking framework for regression, leveraging meta-decision trees and innovative meta-features to perform on-demand selection of base learners. The empirical evaluation confirms its effectiveness in addressing model integration problems. Future work will focus on refining model generation strategies and addressing computational complexity considerations.