DiCE: The Infinitely Differentiable Monte-Carlo Estimator (1802.05098v3)

Abstract: The score function estimator is widely used for estimating gradients of stochastic objectives in stochastic computation graphs (SCG), eg, in reinforcement learning and meta-learning. While deriving the first-order gradient estimators by differentiating a surrogate loss (SL) objective is computationally and conceptually simple, using the same approach for higher-order derivatives is more challenging. Firstly, analytically deriving and implementing such estimators is laborious and not compliant with automatic differentiation. Secondly, repeatedly applying SL to construct new objectives for each order derivative involves increasingly cumbersome graph manipulations. Lastly, to match the first-order gradient under differentiation, SL treats part of the cost as a fixed sample, which we show leads to missing and wrong terms for estimators of higher-order derivatives. To address all these shortcomings in a unified way, we introduce DiCE, which provides a single objective that can be differentiated repeatedly, generating correct estimators of derivatives of any order in SCGs. Unlike SL, DiCE relies on automatic differentiation for performing the requisite graph manipulations. We verify the correctness of DiCE both through a proof and numerical evaluation of the DiCE derivative estimates. We also use DiCE to propose and evaluate a novel approach for multi-agent learning. Our code is available at https://www.github.com/alshedivat/lola.

• The paper introduces DiCE, a novel estimator that computes any order gradient in stochastic computation graphs using the MagicBox operator.
• It efficiently computes gradients and Hessians, with experiments demonstrating high accuracy on iterated prisoner's dilemma and stabilized multi-agent RL outcomes.
• DiCE replaces error-prone surrogate loss methods by enabling automated differentiation and efficient variance reduction in reinforcement learning and meta-learning.

DiCE: The Infinitely Differentiable Monte-Carlo Estimator

Introduction

The paper introduces DiCE, an estimator that overcomes significant limitations of the surrogate loss method in the context of stochastic computation graphs (SCGs), particularly focusing on higher-order derivatives. The surrogate loss (SL) method is insufficient for higher-order derivatives primarily due to its approach of treating parts of the cost as fixed samples. This method results in missing or incorrect terms when calculating these higher-order derivatives. DiCE addresses these issues with a novel operator, the MagicBox, enabling infinitely differentiable estimation using automatic differentiation and aiding practical applications in reinforcement learning (RL) and meta-learning.

Methodology

DiCE provides a unique approach to calculating gradients in SCGs by constructing a single objective that is differentiable to any order. The MagicBox operator, central to DiCE, handles stochastic nodes influenced by parameters. When differentiated, this operator reconstructs necessary gradient dependencies normally lost in surrogate cost approaches. DiCE replaces labor-intensive and error-prone analytical methods with automated systems compatible with deep learning frameworks such as TensorFlow and PyTorch.

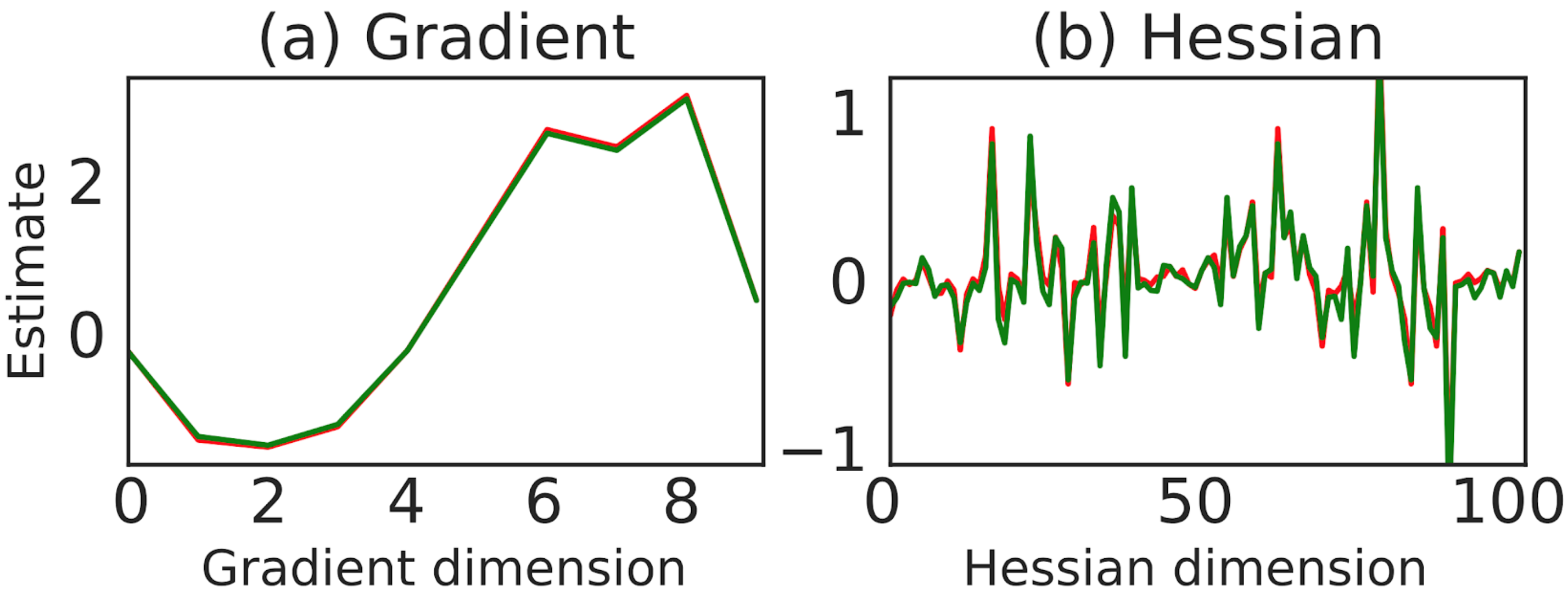
Figure 1: For the iterated prisoner's dilemma, shown is the flattened true (red) and estimated (green) gradient (left) and Hessian (right) using the first and second derivative of DiCE and the exact value function respectively.

Implementation and Empirical Results

DiCE includes a baseline mechanism for variance reduction and supports efficient computation of Hessian-vector products. This implementation enables researchers to apply high order learning methods flexibly across various domains. The empirical studies using DiCE in iterated prisoner's dilemma (IPD) games show high accuracy, with DiCE recovering both gradients and Hessians effectively. DiCE’s implementation in multi-agent RL through Lookahead Opponent Learning Awareness (LOLA) demonstrated stabilized learning outcomes even with significantly smaller batch sizes.

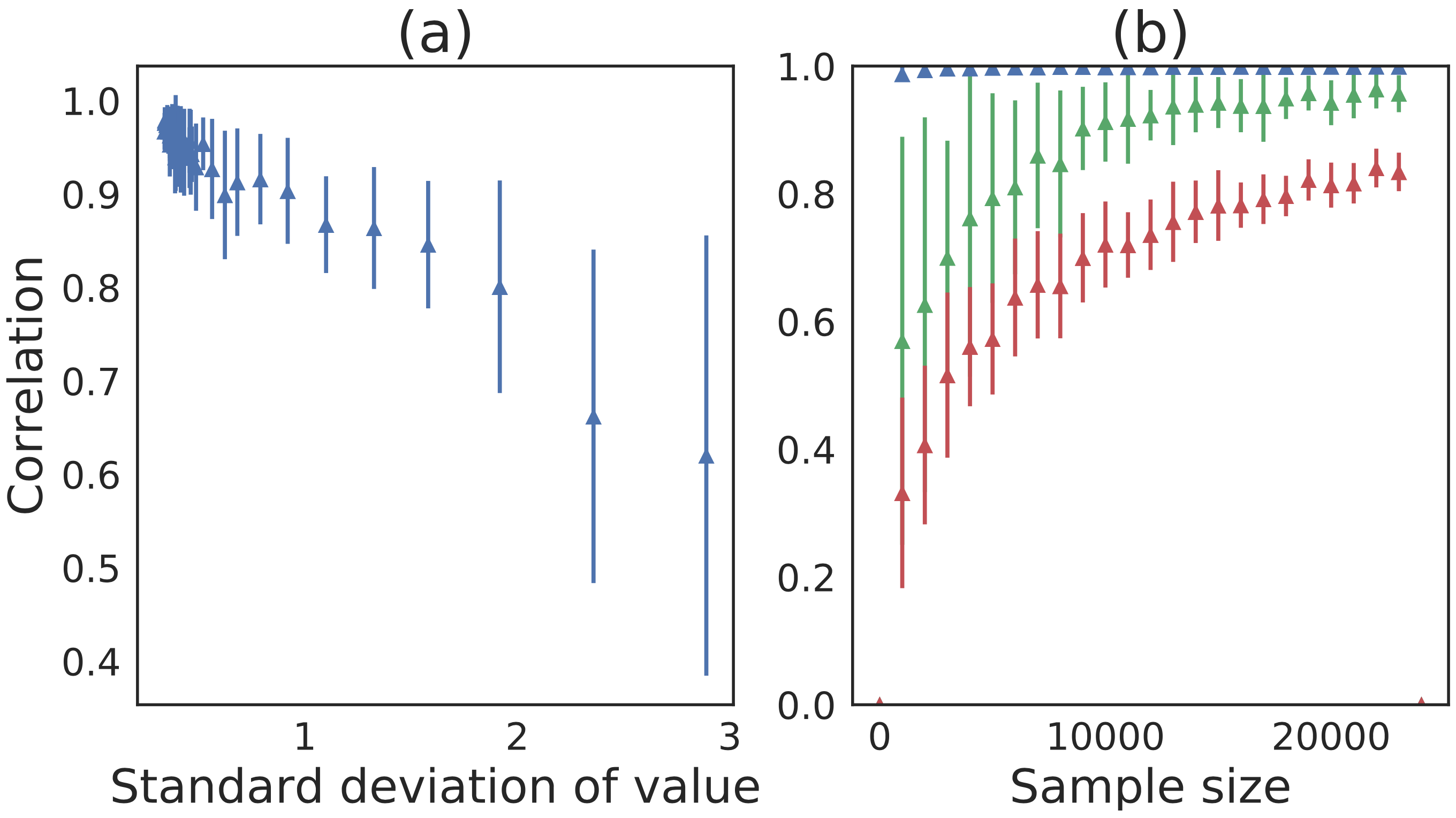
Figure 2: Shown in (a) is the correlation of the gradient estimator (averaged across agents) as a function of the estimation error of the baseline when using a sample size of 128; (b) shows that the quality of the gradient estimation improves with sample size and baseline use.

Discussion

DiCE's flexibility extends to complex game scenarios where differentiating through learning steps of one agent by another provides strategic advantages. By opening pathways to higher-order derivatives without the SL approach's cumbersome methods, DiCE widens exploration within fields like meta-learning and beyond. It directly challenges previous methods that demanded manual higher-order derivative estimation or computational overhead, ultimately encouraging broader application and research in efficient training strategies.

Conclusion

DiCE is a robust solution for estimating any order gradient in SCGs, combining practical implementability with theoretical soundness. It effectively resolves SL approach limitations while supporting higher order learning and variance reduction techniques. As an integrative framework for implementing advanced learning methodologies in AI research, DiCE facilitates enhanced strategies in RL and meta-learning contexts, promising further innovative developments in the computational modeling and optimization domains.