A Novel Weighted Distance Measure for Multi-Attributed Graph (1801.07150v1)

Abstract: Due to exponential growth of complex data, graph structure has become increasingly important to model various entities and their interactions, with many interesting applications including, bioinformatics, social network analysis, etc. Depending on the complexity of the data, the underlying graph model can be a simple directed/undirected and/or weighted/un-weighted graph to a complex graph (aka multi-attributed graph) where vertices and edges are labelled with multi-dimensional vectors. In this paper, we present a novel weighted distance measure based on weighted Euclidean norm which is defined as a function of both vertex and edge attributes, and it can be used for various graph analysis tasks including classification and cluster analysis. The proposed distance measure has flexibility to increase/decrease the weightage of edge labels while calculating the distance between vertex-pairs. We have also proposed a MAGDist algorithm, which reads multi-attributed graph stored in CSV files containing the list of vertex vectors and edge vectors, and calculates the distance between each vertex-pair using the proposed weighted distance measure. Finally, we have proposed a multi-attributed similarity graph generation algorithm, MAGSim, which reads the output of MAGDist algorithm and generates a similarity graph that can be analysed using classification and clustering algorithms. The significance and accuracy of the proposed distance measure and algorithms is evaluated on Iris and Twitter data sets, and it is found that the similarity graph generated by our proposed method yields better clustering results than the existing similarity graph generation methods.

• The paper introduces a novel weighted distance measure that integrates vertex and edge attributes using a weighted Euclidean norm.
• It presents the MAGDist and MAGSim algorithms, which improve clustering accuracy compared to traditional methods on datasets like Iris and Twitter.
• Experimental results show reduced misclassification and enhanced cluster cohesion, indicating potential applications in social media and citation networks.

A Novel Weighted Distance Measure for Multi-Attributed Graphs

Introduction

The paper introduces a novel weighted distance measure designed for multi-attributed graphs where both vertices and edges are represented as multi-dimensional vectors. This metric, based on the weighted Euclidean norm, facilitates graph analysis tasks such as classification and clustering by incorporating both vertex and edge attributes. The proposed framework includes the MAGDist algorithm for calculating distances and the MAGSim algorithm for generating similarity graphs, ultimately improving clustering outcomes over traditional methods.

Methodology

Weighted Distance Measure

The distance measure leverages the weighted Euclidean norm to compute distances between vertices in a multi-attributed graph. This is achieved by accounting for both vertex and edge attributes, enabling a nuanced understanding of the graph's structure. The proposed method utilizes a scalar $\lambda$, derived from the aggregate weight of edges between vertex pairs, allowing the model to modulate the influence of edge attributes.

The formulation is as follows:

1. Distance Input: For vertices $u$ and $v$, and edge attributes $e_{1}, e_{2}, \ldots, e_{m}$.
2. Aggregate Weight: Calculated by equation (12), where weights $\alpha_i$ contribute to the edge influence.
3. Distance Calculation: The distance $\Delta(u, v)$ is computed using equation (10), adjusting vertex separation by edge weights.

Algorithms

• MAGDist: Calculates the pairwise distances within the graph:

  def MAGDist(vertex_data, edge_data, alpha, gamma): # Calculate distances considering vertex and edge weights # Returns a CSV file with distances between vertex pairs

• MAGSim: Utilizes the distances from MAGDist to create a similarity graph:

  def MAGSim(distance_data): # Convert distances to similarity scores # Returns a CSV file representing the similarity graph

Experimental Evaluation

The proposed methodology was evaluated on several datasets:

1. Iris Dataset: Modeled as a multi-attributed graph (Figures 4 and 5).
2. Twitter Dataset: Tweaked for heterogeneous data analysis with real social media data (Figures 8 and 9).

The results denote that MAGSim-generated similarity graphs facilitate superior clustering accuracy when compared to traditional methods like Gaussian kernel or $k$-nn.

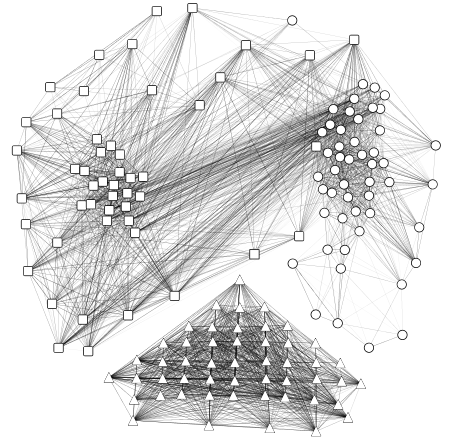
Figure 1: $G_1$: Iris data graph modeled as a multi-attributed graph with Gaussian similarity.

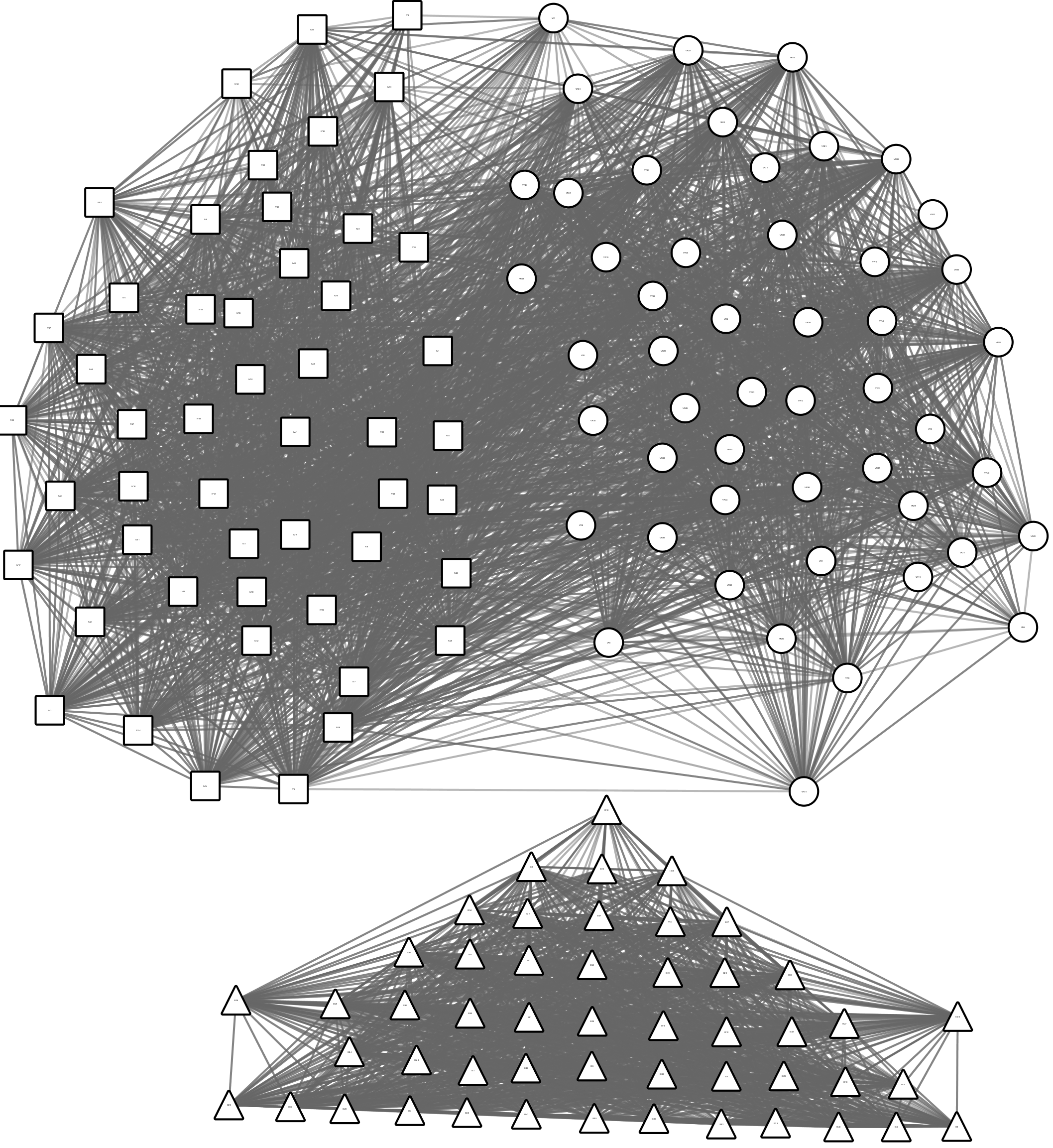
Figure 2: $G_2$: Iris data graph with MAGSim similarity calculated using equation (14).

Clustering Results

Applying the Markov Clustering (MCL) algorithm on similarity graphs derived from MAGDist revealed improved classification accuracy for different data categories. The Iris data clustering (Figures 6 and 7) demonstrated reduced misclassification rates and enhanced cluster cohesion.

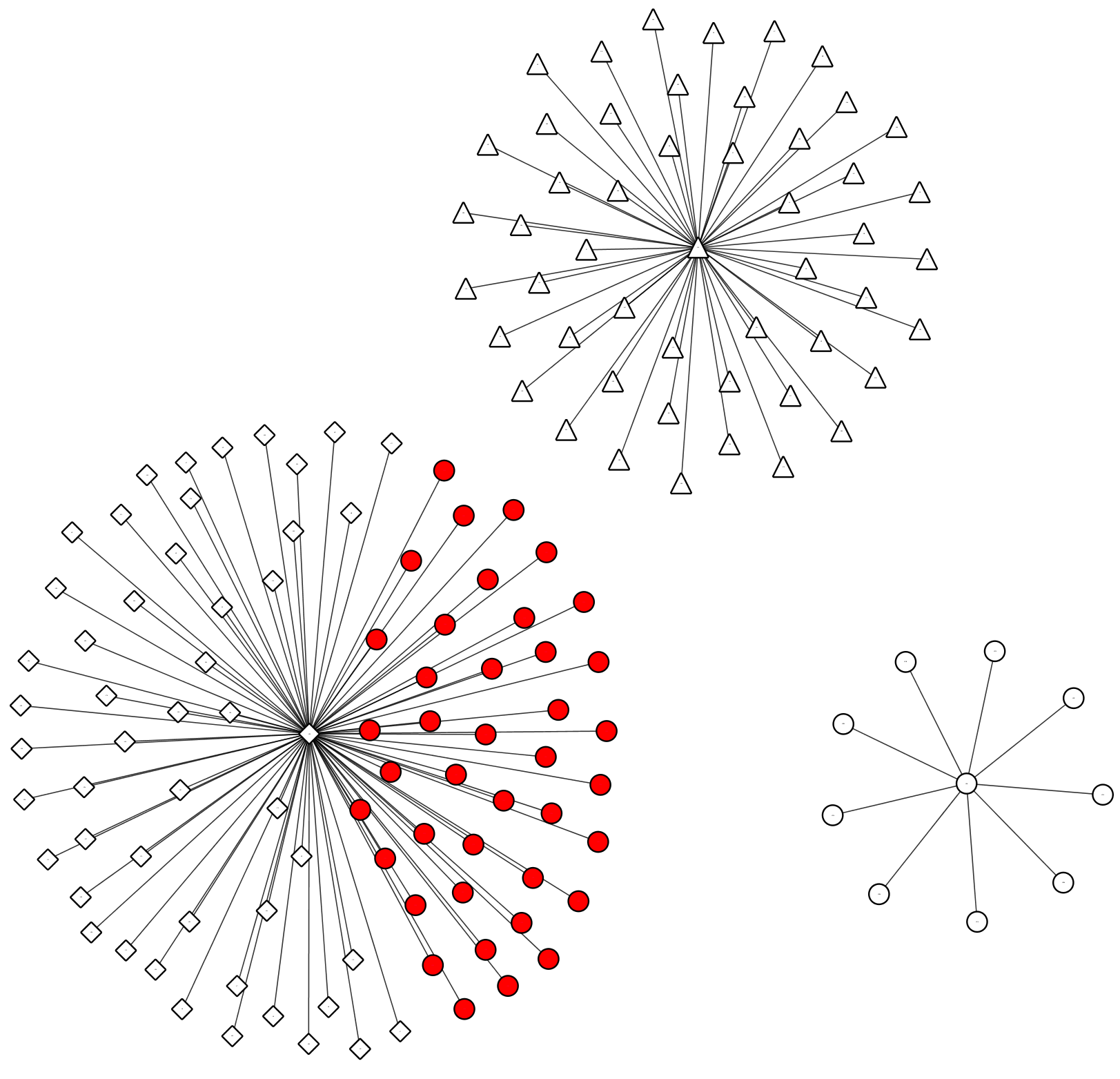
Figure 3: Clustering results after applying MCL over the Iris data graph $G_1$.

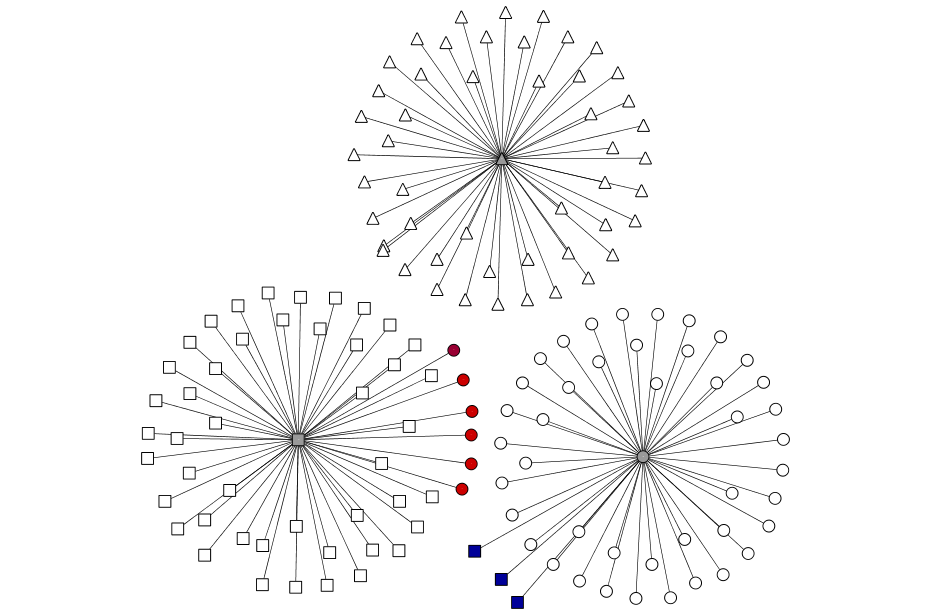
Figure 4: Clustering results after applying MCL over the Iris data graph $G_2$.

Conclusion

The paper presents a significant enhancement in handling multi-attributed graphs by developing a measure that efficiently incorporates both vertex and edge attributes. The MAGDist and MAGSim algorithms successfully transform complex, multi-dimensional data into simplified representations, enabling proficient clustering and classification. Future directions include scaling the approach for large graph datasets and applying it to domains like citation networks and social media analysis, which demand multi-faceted graph interpretations.