Metrics for Deep Generative Models (1711.01204v2)

Abstract: Neural samplers such as variational autoencoders (VAEs) or generative adversarial networks (GANs) approximate distributions by transforming samples from a simple random source---the latent space---to samples from a more complex distribution represented by a dataset. While the manifold hypothesis implies that the density induced by a dataset contains large regions of low density, the training criterions of VAEs and GANs will make the latent space densely covered. Consequently points that are separated by low-density regions in observation space will be pushed together in latent space, making stationary distances poor proxies for similarity. We transfer ideas from Riemannian geometry to this setting, letting the distance between two points be the shortest path on a Riemannian manifold induced by the transformation. The method yields a principled distance measure, provides a tool for visual inspection of deep generative models, and an alternative to linear interpolation in latent space. In addition, it can be applied for robot movement generalization using previously learned skills. The method is evaluated on a synthetic dataset with known ground truth; on a simulated robot arm dataset; on human motion capture data; and on a generative model of handwritten digits.

• The paper presents a Riemannian metric to compute geodesic distances in latent spaces, enabling smoother sample interpolation and better manifold understanding.
• It leverages Importance-Weighted Autoencoders and deep generative frameworks to improve model performance on datasets like MNIST and robotic motion data.
• Experimental results across synthetic pendulum, robotic, and human motion datasets validate the method’s effectiveness in real-world applications such as path planning and data harmonization.

Metrics for Deep Generative Models

This paper presents a method to enhance the utility of latent variable models used in deep generative frameworks, specifically focusing on variational autoencoders (VAEs) and generative adversarial networks (GANs). It leverages concepts from Riemannian geometry to introduce a principled distance measure in latent spaces, which can significantly improve interpolation between samples and offer insights into the learned data manifold structure.

Introduction and Motivation

Deep generative models transform simple random samples from a latent space into complex distributions resembling real-world datasets. However, typical training objectives tend to densely fill the latent space, resulting in suboptimal distance measures where separations in observation space do not align with those in the latent space. The proposed solution involves using Riemannian geometry to redefine these distances as geodesics—shortest paths along a learned manifold—providing a more meaningful measure that captures inherent similarities between data points more accurately than Euclidean metrics.

Riemannian Geometry in Latent Space

The latent space is treated as a Riemannian manifold, allowing for the measurement of distances using shortest paths rather than straight linear interpolations. This approach compensates for the discontinuities and dense coverage in the latent space that can distort similarity measures. The process involves approximating the geodesics between points, which are computed by minimizing the length of curves that are parameterized by a function from the latent space to the observation space.

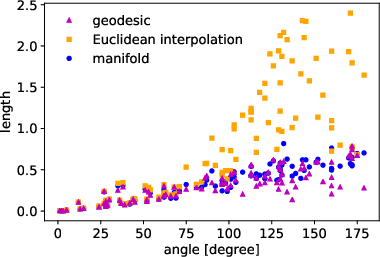
Figure 1: The horizontal axis is the angle between the starting and end points. The average of the length of the geodesics, the Euclidean interpolations, and the paths along the data manifold are 0.319, 0.820, and 0.353 respectively.

Methodology

Importance-Weighted Autoencoder

An ideal generative model for this approach is the Importance-Weighted Autoencoder (IWAE), which uses importance sampling to propose latent distributions. This tighter lower bound on the evidence allows capturing more complex latent structures, providing a robust basis for applying Riemannian metrics and smoothing the manifold with techniques like singular-value decomposition (SVD).

Implementing Riemannian Distances

The computation of geodesics between data points involves neural networks that approximate the parametric curves within the latent space. The solution applies boundary constraints and employs a regularization term to ensure smoother integration along the manifold. This is achieved by penalizing the metric tensor and leveraging SVD for optimizing the manifold representation.

Experiments

Artificial Pendulum Dataset

The application on a synthetic pendulum dataset demonstrates the efficacy of geodesic interpolation producing consistently smoother transitions compared to Euclidean interpolation. The results are quantitatively evaluated with the regularization impact illustrated.

MNIST Dataset

On the MNIST dataset, geodesics allowed differentiation of classes within the latent space that was otherwise indistinct when using Euclidean measures. This differentiation is particularly useful for downstream tasks like class separation crucial for classification models.

Robotic Applications

The method was evaluated on simulated robot arm motion data, where geodesics provided smoother, more natural motion trajectories. This capability is pivotal for robotic path planning and executing learned tasks with high precision and minimal computational overhead.

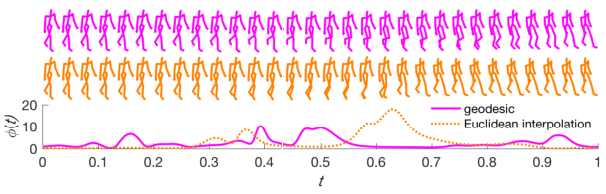
Figure 2: The reconstructions of the geodesic and Euclidean interpolation of the human motion. Top row: mean of the reconstruction from the geodesic. Middle row: mean of the reconstruction from the Euclidean interpolation. Bottom row: velocity (Eq.~(\ref{eq:velocity}).

Human Motion Dataset

The approach was further validated on human motion data, showcasing its potential in domains requiring high-dimensional data harmonization and continuity in observations. The geodesic paths resulted in more coherent and continuous motion representations compared to linear interpolations.

Conclusion

The paper introduces a novel Riemannian distance metric for latent spaces of deep generative models, resolving the common issue of unreliable similarity measures in high-dimensional spaces. This technique enhances model interpretability, provides a more accurate distance measure that aligns better with the manifold hypothesis, and facilitates applications in robotic path planning and complex data interpolation. Future research could explore dynamic model extensions and integration into active learning environments for continuous data adaptation and learning.