Cell Detection in Microscopy Images with Deep Convolutional Neural Network and Compressed Sensing (1708.03307v3)

Abstract: The ability to automatically detect certain types of cells or cellular subunits in microscopy images is of significant interest to a wide range of biomedical research and clinical practices. Cell detection methods have evolved from employing hand-crafted features to deep learning-based techniques. The essential idea of these methods is that their cell classifiers or detectors are trained in the pixel space, where the locations of target cells are labeled. In this paper, we seek a different route and propose a convolutional neural network (CNN)-based cell detection method that uses encoding of the output pixel space. For the cell detection problem, the output space is the sparsely labeled pixel locations indicating cell centers. We employ random projections to encode the output space to a compressed vector of fixed dimension. Then, CNN regresses this compressed vector from the input pixels. Furthermore, it is possible to stably recover sparse cell locations on the output pixel space from the predicted compressed vector using $L_1$-norm optimization. In the past, output space encoding using compressed sensing (CS) has been used in conjunction with linear and non-linear predictors. To the best of our knowledge, this is the first successful use of CNN with CS-based output space encoding. We made substantial experiments on several benchmark datasets, where the proposed CNN + CS framework (referred to as CNNCS) achieved the highest or at least top-3 performance in terms of F1-score, compared with other state-of-the-art methods.

• The paper presents CNNCS, a framework that encodes sparse cell locations into compressed vectors and recovers them via L1-norm minimization.
• It integrates deep CNN regression using architectures like AlexNet and ResNet with multi-task learning to enhance detection accuracy.
• The method is theoretically justified using the restricted isometry property and empirically outperforms traditional techniques across multiple datasets.

Deep Convolutional Neural Network and Compressed Sensing for Cell Detection in Microscopy Images

Introduction

The paper presents a novel framework, CNNCS, for cell detection and localization in microscopy images, integrating deep convolutional neural networks (CNNs) with compressed sensing (CS)-based output encoding. The approach addresses the inherent sparsity of cell locations in high-resolution images and the limitations of direct pixel-space classification, particularly the class imbalance and susceptibility to false positives. By encoding cell locations into a compressed vector via random projections and regressing this vector from image data using a CNN, the method leverages $L_1$-norm optimization for robust recovery of cell centroids. This paradigm shift from direct coordinate prediction to compressed signal regression is theoretically justified by the restricted isometry property (RIP) of CS and is empirically validated on multiple benchmark datasets.

Figure 1: Microscopy image with annotated mitotic cells and examples of mitotic figures.

Methodology

System Architecture

The CNNCS framework comprises three principal stages: (1) cell location encoding via random projection, (2) CNN-based regression to predict the compressed signal, and (3) decoding through $L_1$-norm minimization to recover cell locations. The encoding transforms the sparse binary annotation map of cell centroids into a fixed-length compressed vector, which serves as the regression target for the CNN. Two encoding schemes are proposed: Scheme-1 (reshaping the annotation map) and Scheme-2 (encoding signed distances to multiple observation axes), with Scheme-2 offering significant computational advantages and redundancy for improved detection reliability.

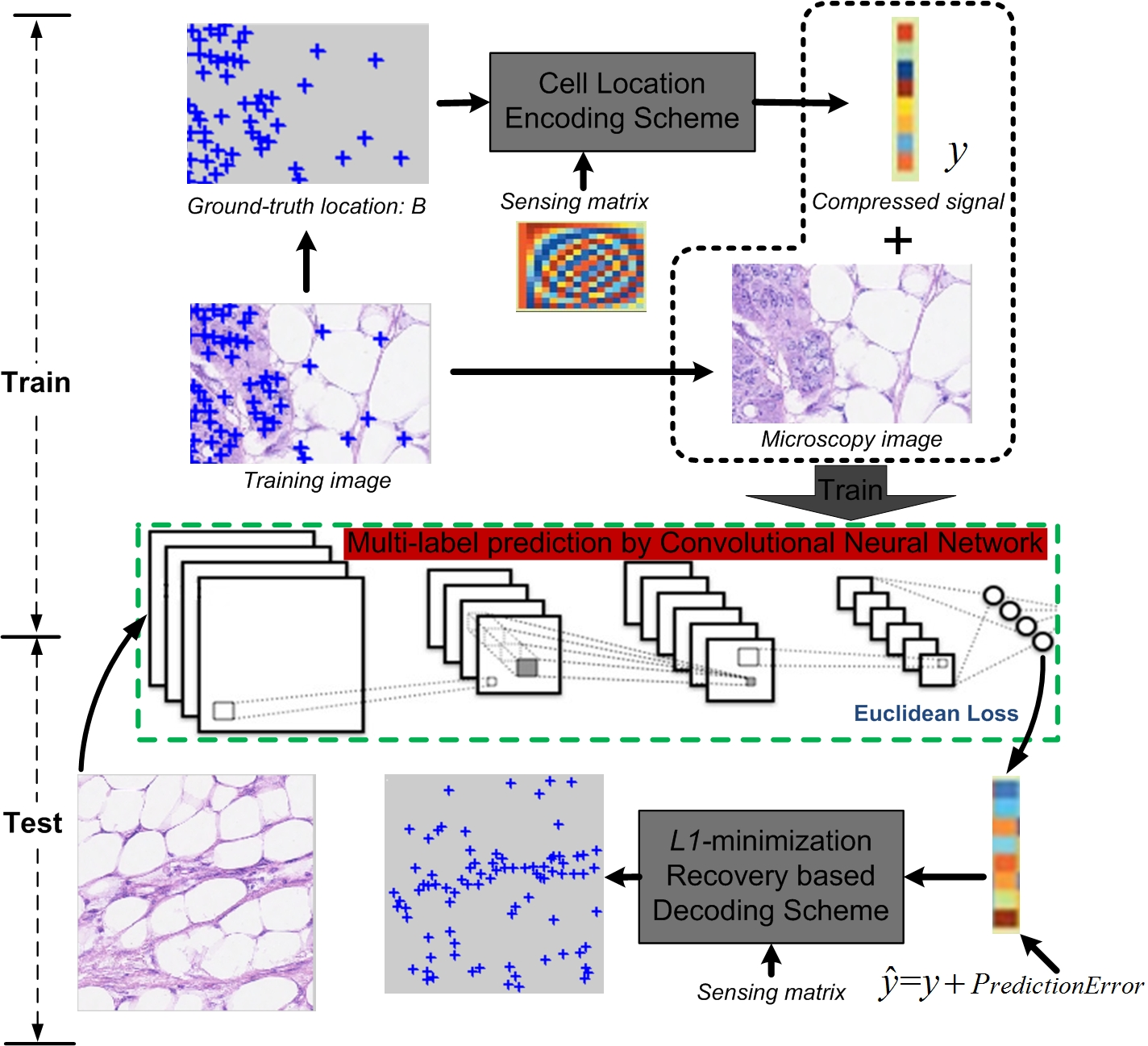
Figure 2: Overview of the CNNCS framework for cell detection and localization.

Encoding and Decoding

Scheme-1 concatenates the binary annotation map into a sparse vector, which is then projected using a random Gaussian matrix. Scheme-2 projects cell centroids onto multiple uniformly distributed axes, encoding their signed distances and concatenating the results. The latter reduces the dimensionality of the sensing matrix and introduces redundancy, facilitating robust recovery. Decoding is performed via $L_1$-norm convex optimization, followed by mean shift clustering to aggregate candidate detections and suppress noise.

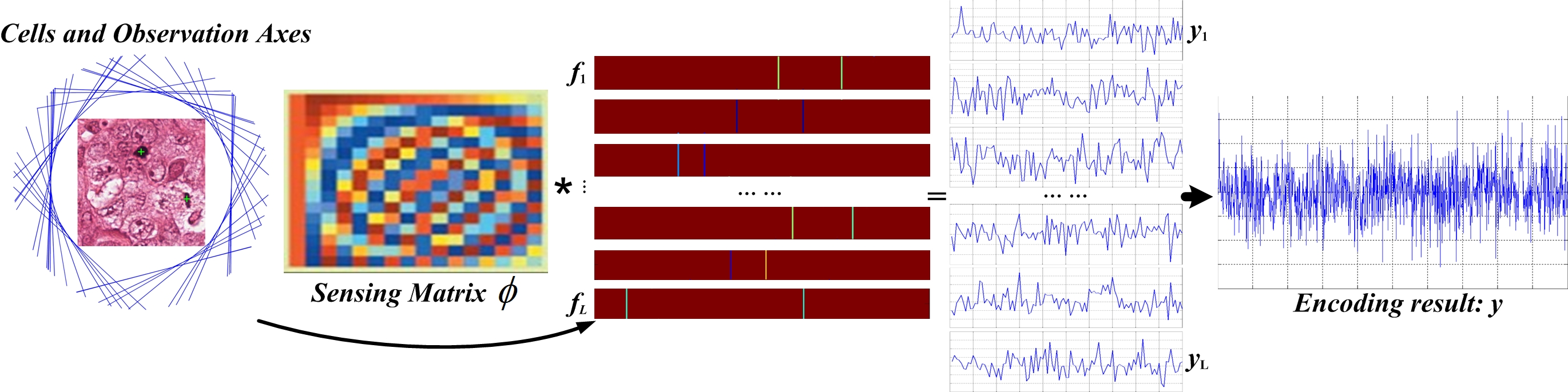
Figure 3: Cell location encoding by signed distances (Scheme-2).

Figure 4: Decoding scheme illustrating true and recovered location signals and final detection results.

CNN Regression and Multi-Task Learning

The regression model utilizes AlexNet and ResNet architectures, with the output layer dimension matching the compressed signal length. Training employs Euclidean loss, and data augmentation via patch rotation enhances robustness. Multi-task learning (MTL) is incorporated by fusing cell count information with the compressed signal, further optimizing detection and counting performance.

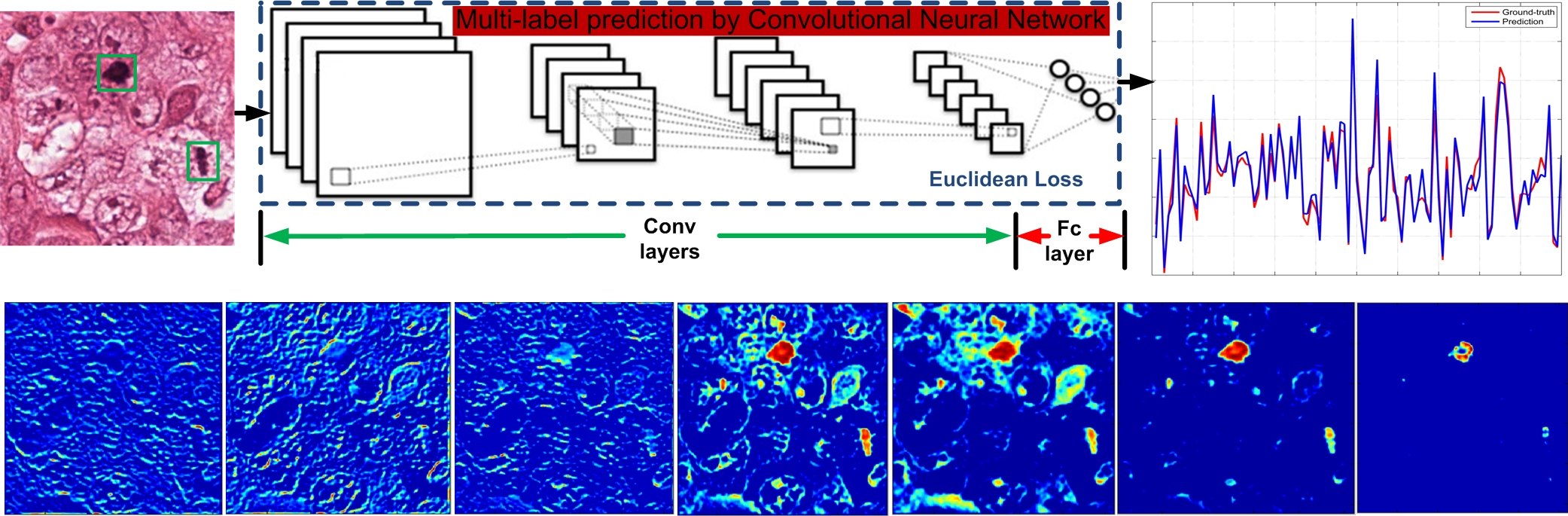
Figure 5: Signal prediction process and feature maps from CNN layers, showing close approximation of ground-truth and predicted compressed signals.

Theoretical Analysis

The equivalence of optimization targets in compressed and original pixel spaces is established via the RIP of the sensing matrix. The generalization error bound demonstrates that the expected error in cell localization is controlled by the predictor's error in compressed space and the reconstruction algorithm's error, justifying the use of deep CNNs and advanced $L_1$ recovery methods.

Experimental Results

Datasets and Evaluation

Seven datasets, including ICPR 2012/2014, AMIDA 2013/2016, and others, are used for evaluation. The annotation format and dataset diversity are illustrated below.

Figure 6: Examples of datasets and their cell centroid annotations.

Performance is measured using precision, recall, and F1-score, with detection considered correct if the predicted centroid lies within a specified radius of the ground truth.

Comparative Analysis

Scheme-1 Results

CNNCS with Scheme-1 outperforms traditional methods (FCN-based, Le.detect, CasNN) in precision-recall curves, particularly at higher recall values, due to its robustness against prediction bias and error in dense cell scenarios.

Scheme-2 Results

On the ICPR 2012 dataset, CNNCS-ResNet-MTL achieves the highest F1-score (0.837), surpassing previous state-of-the-art methods. The redundancy in Scheme-2 encoding and ensemble averaging contribute to improved precision and recall. On the ICPR 2014 dataset, CNNCS nearly doubles the F1-score of the second-best team (0.633 vs. 0.356). On AMIDA 2013/2016, CNNCS consistently ranks in the top three, demonstrating generalizability across diverse histology images and cell types.

Discussion

The integration of compressed sensing with deep CNNs for output space encoding represents a significant methodological advancement for sparse object detection tasks. The approach mitigates class imbalance and leverages the theoretical guarantees of CS for stable recovery. The redundancy in Scheme-2 encoding and ensemble averaging strategies further enhance detection reliability, particularly in challenging, high-density scenarios. The empirical results indicate that CNNCS is competitive with, and often superior to, existing methods across multiple datasets and contest benchmarks.

The framework's modularity allows for the adoption of advanced CNN architectures and multi-task learning, suggesting potential for further improvements via end-to-end training and more sophisticated ensemble techniques. The theoretical analysis provides a foundation for extending the approach to other sparse detection problems in medical imaging and beyond.

Conclusion

The CNNCS framework demonstrates that deep convolutional neural networks, when combined with compressed sensing-based output encoding, can effectively address the challenges of cell detection and localization in microscopy images. The method achieves top-tier performance on multiple benchmarks, with strong theoretical justification and practical advantages in memory efficiency and robustness. Future work may focus on fully end-to-end training and adaptation to other domains requiring sparse object detection.