SmoothGrad: removing noise by adding noise (1706.03825v1)

Abstract: Explaining the output of a deep network remains a challenge. In the case of an image classifier, one type of explanation is to identify pixels that strongly influence the final decision. A starting point for this strategy is the gradient of the class score function with respect to the input image. This gradient can be interpreted as a sensitivity map, and there are several techniques that elaborate on this basic idea. This paper makes two contributions: it introduces SmoothGrad, a simple method that can help visually sharpen gradient-based sensitivity maps, and it discusses lessons in the visualization of these maps. We publish the code for our experiments and a website with our results.

• The paper introduces SmoothGrad, which improves noisy sensitivity maps by averaging gradients from multiple noise-perturbed images.
• Experimental results using models like Inception v3 and MNIST demonstrate that SmoothGrad significantly enhances visual coherence and feature alignment.
• The method integrates seamlessly with other gradient attribution techniques, offering practical benefits for model debugging and interpretability in sensitive applications.

Introduction to SmoothGrad Methodology

The paper "SmoothGrad: Removing Noise by Adding Noise" proposes a method to enhance the interpretability of sensitivity maps generated by deep image classification networks. These sensitivity maps, derived from the gradients of class activation functions, often suffer from visual noise. The authors introduce SmoothGrad, a technique that improves the clarity of these maps by averaging the maps derived from images perturbed with Gaussian noise.

Gradient-Based Sensitivity Maps

Gradient-based sensitivity maps, denoted as $M_c(x) = \partial S_c(x) / \partial x$, provide a fundamental method to elucidate the pixel-level importance of an input image $x$ for a classification score $S_c(x)$. Despite their utility in theory, these maps frequently appear visually noisy when presented to human observers (Figure 1).

Figure 1: A noisy sensitivity map, based on the gradient of the class score for gazelle for an image classification network. Lighter pixels indicate partial derivatives with higher absolute values.

Several strategies have been historically applied to mitigate this noise, such as Layerwise Relevance Propagation, Integrated Gradients, and Guided Backpropagation. These methods aim to refine the attribution of pixel importance in a way that aligns more closely with intuitive human understanding.

Smoothing Noisy Gradients with SmoothGrad

The key insight of the SmoothGrad approach is recognizing that sharp fluctuations in partial derivatives may contribute to the noise observed in sensitivity maps. The method involves averaging the sensitivity maps generated from multiple noise-perturbed versions of the same image:

$$\hat{M_c}(x) = \frac{1}{n} \sum_1^n M_c(x + \mathcal{N}(0, \sigma^2))$$

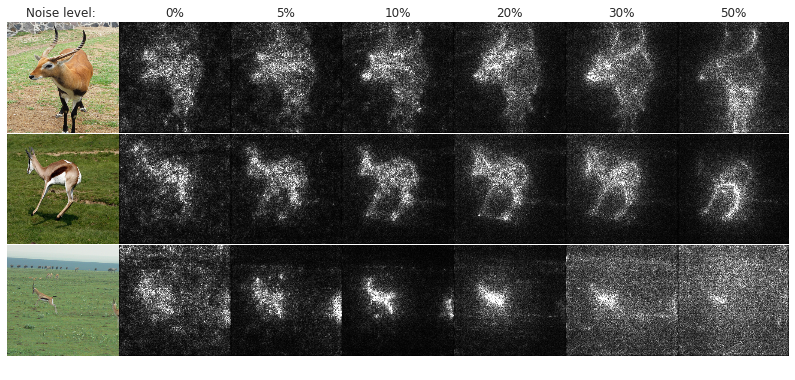
Figure 2: Effect of noise level (columns) on our method for 5 images of the gazelle class in ImageNet (rows). Each sensitivity map is obtained by applying Gaussian noise $\mathcal{N}(0,\,\sigma^{2})$.

This stochastic approximation significantly enhances the visual coherence of sensitivity maps without necessitating changes to the network architecture.

Experimental Validation

Experiments conducted using models such as Inception v3 and a convolutional MNIST model validate the efficacy of SmoothGrad. By adjusting noise levels and sample sizes during inference, the authors demonstrate a marked improvement in the alignment of sensitivity maps with meaningful image features (Figure 3).

Figure 3: Effect of sample size on the estimated gradient for inception. 10\% noise was applied to each image.

Qualitative comparisons indicate that SmoothGrad surpasses other baseline methods in providing visually coherent and discriminative sensitivity maps (Figure 4).

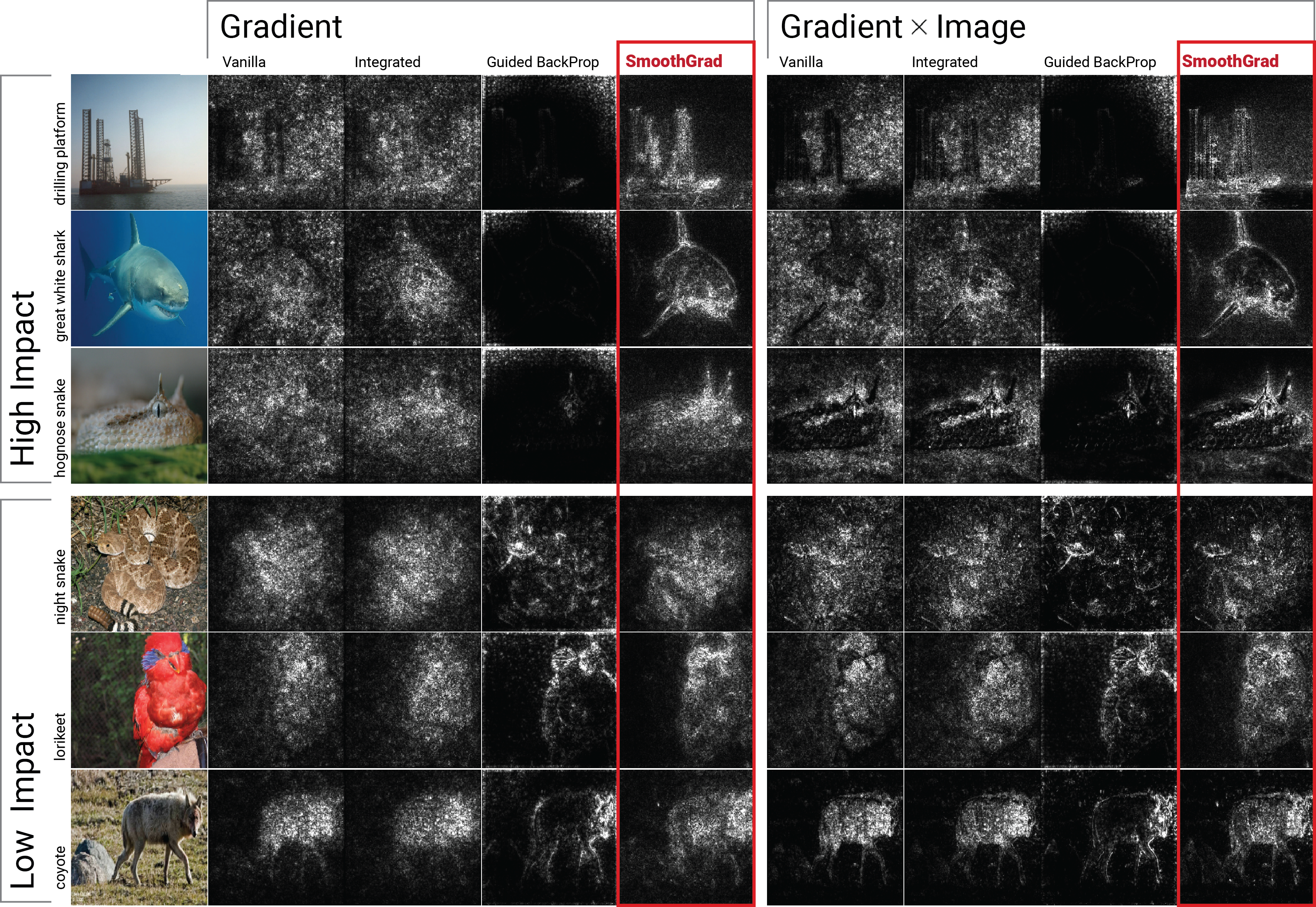
Figure 4: Qualitative evaluation of different methods. First three (last three) rows show examples where applying SmoothGrad had high (low) impact on the quality of sensitivity map.

Integration with Existing Methods

SmoothGrad can be combined with other gradient refinement methods like Integrated Gradients and Guided BackProp to further enhance sensitivity map clarity and coherence (Figure 5).

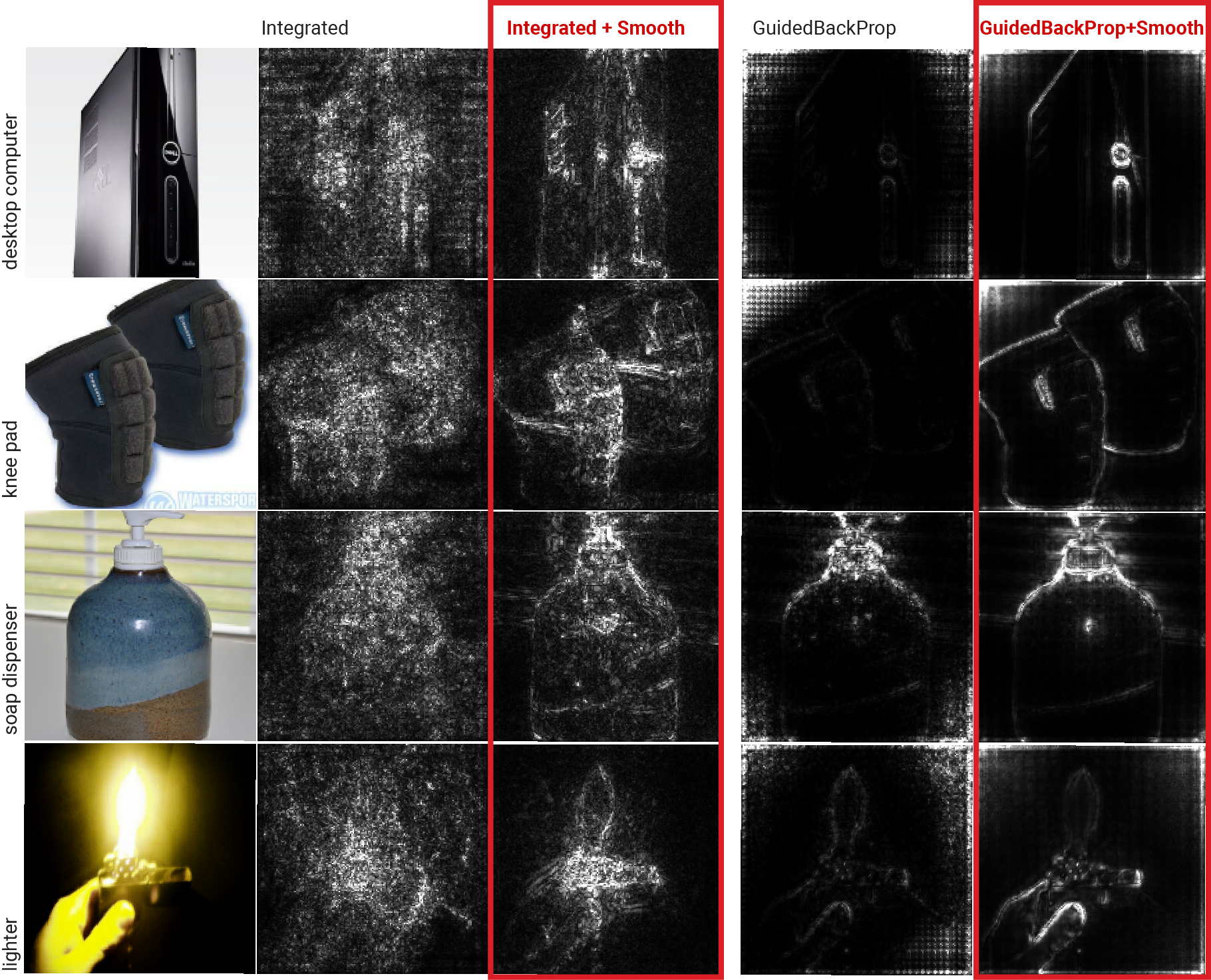
Figure 5: Using SmoothGrad in addition to existing gradient-based methods: Integrated Gradients and Guided BackProp.

Implications and Future Directions

SmoothGrad represents a significant advancement in sensitivity map visualization, offering an easily implementable means of reducing noise through perturbation and averaging. The implications for real-world applications are profound, with potential benefits in model debugging and in meeting interpretability requirements in sensitive domains such as healthcare.

Future research may explore deeper theoretical justifications for the efficacy of SmoothGrad, investigate differential impacts based on image texture and pixel distribution, and propose quantitative metrics for evaluating sensitivity maps. Additionally, examining the application of SmoothGrad across different architectures and tasks could broaden its utility.

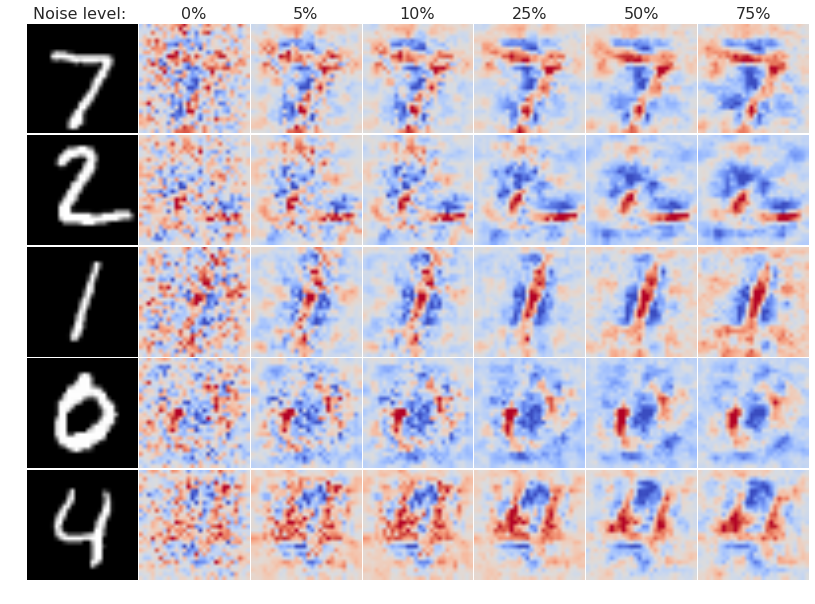
Figure 6: Effect of noise level on the estimated gradient across 5 MNIST images. Each sensitivity map is obtained by applying a Gaussian noise at inference time and averaging.

Conclusion

The SmoothGrad approach effectively mitigates the limitations of noisy sensitivity maps by harnessing noise for enhancement, providing a robust technique applicable to any gradient-based saliency method. This innovative use of stochastic sampling offers a promising avenue for future explorations into model interpretability and accountability in complex machine learning systems.