Sharp Minima Can Generalize For Deep Nets (1703.04933v2)

Abstract: Despite their overwhelming capacity to overfit, deep learning architectures tend to generalize relatively well to unseen data, allowing them to be deployed in practice. However, explaining why this is the case is still an open area of research. One standing hypothesis that is gaining popularity, e.g. Hochreiter & Schmidhuber (1997); Keskar et al. (2017), is that the flatness of minima of the loss function found by stochastic gradient based methods results in good generalization. This paper argues that most notions of flatness are problematic for deep models and can not be directly applied to explain generalization. Specifically, when focusing on deep networks with rectifier units, we can exploit the particular geometry of parameter space induced by the inherent symmetries that these architectures exhibit to build equivalent models corresponding to arbitrarily sharper minima. Furthermore, if we allow to reparametrize a function, the geometry of its parameters can change drastically without affecting its generalization properties.

• The paper demonstrates that reparametrization can produce sharp minima that generalize well despite traditional flatness arguments.
• It critically examines common flatness metrics and reveals their limitations in capturing the non-Euclidean geometry of deep network parameter spaces.
• The study highlights the need for new optimization benchmarks and regularization strategies based on a rigorous understanding of neural network geometry.

Sharp Minima Can Generalize For Deep Nets

This essay explores the research presented in "Sharp Minima Can Generalize For Deep Nets" (1703.04933), analyzing the implications of the paper on the behavior of deep learning networks, particularly in understanding the generalization capabilities of sharp minima. The paper challenges the established notion that flat minima are crucial for good generalization and provides insights into the complexity of parameter space geometry in deep networks.

Introduction

The prevailing hypothesis in deep learning suggests that flat minima of the loss function correlate with better generalization capabilities. This belief stems from the assumption that flat minima provide robustness to noise and model perturbations. However, this paper argues that most definitions of flatness are problematic, particularly for deep networks with rectifier units. The paper explores the geometry of parameter space and shows that arbitrarily sharp minima can be constructed without affecting generalization. It posits that the invariance of generalization in the face of reparametrization challenges the simplicity of the flat minima hypothesis.

Reassessing Minima Flatness

The research revisits common definitions of flatness and sharpness, pointing out their inadequacies in the context of deep neural networks. It particularly highlights the issue that definitions relying on local curvature or regions of low-loss do not adequately capture the generalization behavior due to the non-Euclidean geometry intrinsic to deep neural architectures.

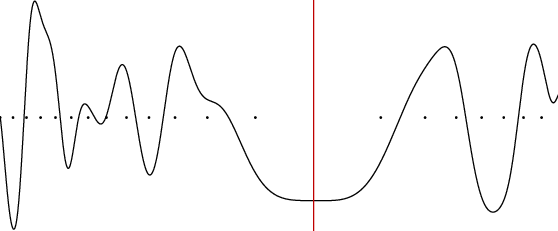
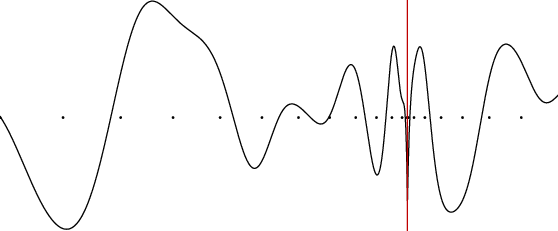
Figure 1: A one-dimensional example on how the geometry of the loss function depends on the parameter space chosen.

Non-Euclidean Geometry in Deep Networks

The paper stresses the importance of considering the unique geometry of parameter spaces in rectified neural networks. Symmetries and non-identifiability inherent in these networks allow transformations that can drastically alter the perceived sharpness of minima, thereby manipulating flatness metrics without real impact on model performance. The invariance under specific transformations undermines traditional views on flatness and sharpness.

The Role of Reparametrization

A key contribution of this paper is demonstrating that reparametrization can create radically different geometric interpretations of the same underlying function. The paper provides examples where minima classified as sharp under one parameterization might appear flat under another, disqualifying simplistic attributions of generalization abilities based solely on curvature representation in parameter space.

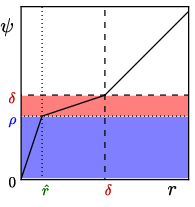
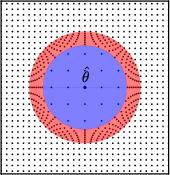
Figure 2: An example of a radial transformation on a 2-dimensional space demonstrating differential area properties.

Practical and Theoretical Implications

The findings necessitate a reevaluation of optimization strategies and the benchmarks used to assess them. Practically, this implies that model selection and regularization strategies relying on the notion of flat minima might be misguided unless grounded in a mathematically rigorous framework that considers the invariance properties highlighted by the paper. Theoretically, it opens new avenues for exploring the dynamics of gradient-based optimization and their relationship to generalization.

Conclusion

"Sharp Minima Can Generalize For Deep Nets" presents a compelling argument that challenges the existing understanding of generalization in deep learning. By underscoring the limitations of current flatness metrics and highlighting the importance of parameter space geometry, the paper invites further exploration into the mathematical underpinnings of learning dynamics and model evaluation. The implications of this research are significant, suggesting that future work should focus on developing more comprehensive approaches to understanding and leveraging the geometry of neural network parameter spaces.