Grammar Variational Autoencoder (1703.01925v1)

Abstract: Deep generative models have been wildly successful at learning coherent latent representations for continuous data such as video and audio. However, generative modeling of discrete data such as arithmetic expressions and molecular structures still poses significant challenges. Crucially, state-of-the-art methods often produce outputs that are not valid. We make the key observation that frequently, discrete data can be represented as a parse tree from a context-free grammar. We propose a variational autoencoder which encodes and decodes directly to and from these parse trees, ensuring the generated outputs are always valid. Surprisingly, we show that not only does our model more often generate valid outputs, it also learns a more coherent latent space in which nearby points decode to similar discrete outputs. We demonstrate the effectiveness of our learned models by showing their improved performance in Bayesian optimization for symbolic regression and molecular synthesis.

• The paper's main contribution is the development of a Grammar Variational Autoencoder that leverages context-free grammars to enforce syntactic validity in generated outputs.
• The GVAE outperforms character-based VAEs by generating higher rates of valid arithmetic expressions and molecules, demonstrating improved latent space quality.
• The approach offers significant implications for optimizing discrete data generation across various domains through robust grammar-based modeling.

Grammar Variational Autoencoder

Introduction

The "Grammar Variational Autoencoder" (1703.01925) paper introduces a novel approach to generative modeling of discrete data, such as arithmetic expressions and molecular structures, by employing grammatical structures. Traditional generative models excel in continuous domains but struggle with the discrete nature of such data, often producing invalid outputs. The proposed method, Grammar Variational Autoencoder (GVAE), addresses this by encoding and decoding parse trees from a context-free grammar, ensuring syntactic correctness and more coherent latent space learning.

Methods

The GVAE employs context-free grammars (CFGs) to define valid structures within the data, such as molecules in SMILES format or arithmetic expressions. By parsing these structures into derivation trees during encoding, and generating parse trees during decoding, the GVAE guarantees syntactic validity. The encoder transforms data sequences into a continuous latent vector using a convolutional neural network, while the decoder outputs valid parse trees using a recurrent neural network with masking to enforce grammar rules.

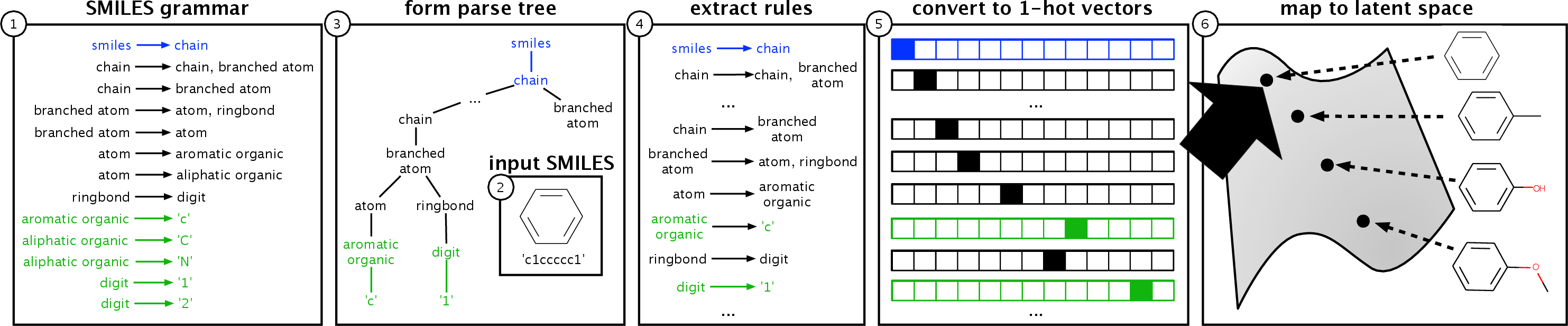
Figure 1: The encoder of the GVAE. We denote the start rule in blue and all rules that decode to terminal in green.

A crucial aspect of the GVAE is its use of a stack-based mechanism during decoding, where a non-terminal symbol is expanded into production rules based on a masked probability distribution derived from the latent vector, ensuring the validity of the generated structures.

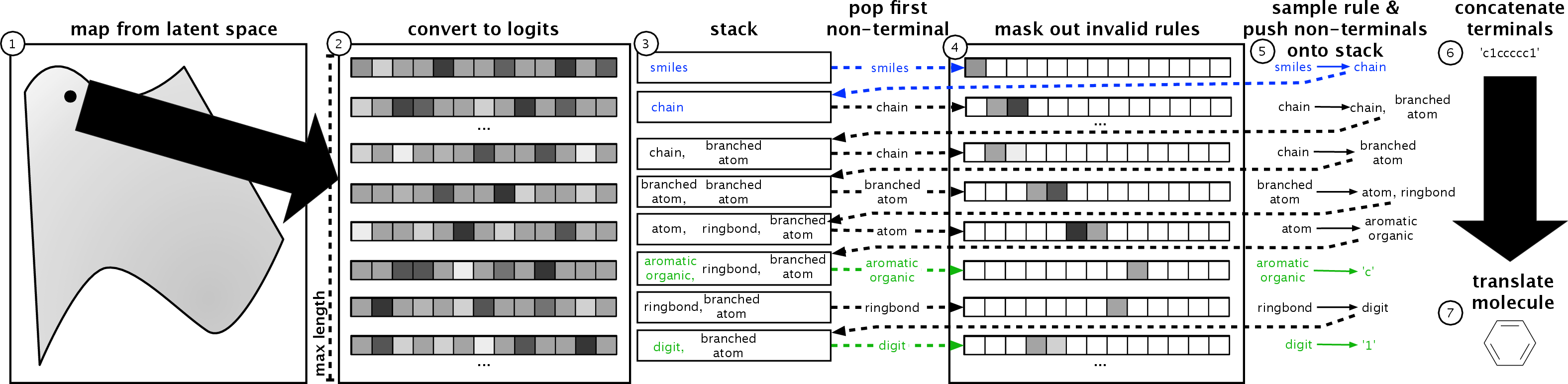
Figure 2: The decoder of the GVAE. See text for details.

Experiments

Arithmetic Expressions

The GVAE was evaluated on tasks such as generating arithmetic expressions and molecules. In arithmetic expression generation, the GVAE outperformed a character-based variational autoencoder (CVAE) by producing a higher percentage of valid expressions and smoother latent space interpolations. This demonstrates the GVAE's ability to learn meaningful latent representations that effectively capture the underlying grammatical structure of the data.

Molecule Generation

For molecular generation, the GVAE showed significant improvements over the CVAE in terms of generating valid molecules and producing higher-quality latent spaces for Bayesian optimization. In particular, the GVAE was more successful at exploring latent spaces to find molecules with desirable properties, such as increased logP values, which are indicative of drug-likeness.

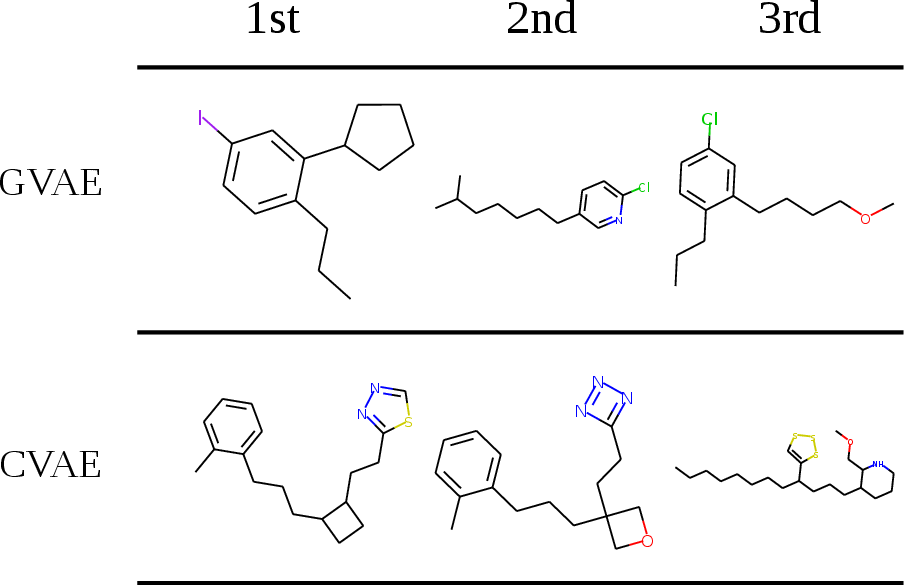
Figure 3: Plot of best molecules found by each method.

Implications and Future Work

The GVAE's approach of incorporating grammatical structures into the generation process not only ensures validity but also enhances the quality of the learned latent space. This method is applicable across various domains where discrete data can be structured using grammars, providing a robust framework for generating valid and semantically meaningful data.

This work opens avenues for further research into grammar-based generative models, particularly in exploring more complex grammars and extending the method to incorporate additional semantic constraints beyond syntactic validity. Future developments may focus on refining these models to address semantic validity further, thereby reducing the generation of chemically implausible molecules or syntactically sound but semantically incorrect arithmetic expressions.

Conclusion

The Grammar Variational Autoencoder represents a significant advancement in the generative modeling of discrete data. By leveraging context-free grammars, the GVAE not only ensures the generation of valid outputs but also fosters the development of a coherent and smooth latent space conducive to optimization tasks. This method holds significant potential for enhancing AI applications in domains reliant on discrete, structured data.