On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima (1609.04836v2)

Abstract: The stochastic gradient descent (SGD) method and its variants are algorithms of choice for many Deep Learning tasks. These methods operate in a small-batch regime wherein a fraction of the training data, say $32$-$512$ data points, is sampled to compute an approximation to the gradient. It has been observed in practice that when using a larger batch there is a degradation in the quality of the model, as measured by its ability to generalize. We investigate the cause for this generalization drop in the large-batch regime and present numerical evidence that supports the view that large-batch methods tend to converge to sharp minimizers of the training and testing functions - and as is well known, sharp minima lead to poorer generalization. In contrast, small-batch methods consistently converge to flat minimizers, and our experiments support a commonly held view that this is due to the inherent noise in the gradient estimation. We discuss several strategies to attempt to help large-batch methods eliminate this generalization gap.

• The paper demonstrates that large-batch training converges to sharp minimizers, resulting in a pronounced generalization gap.
• It employs comprehensive experiments and sharpness metrics across multiple network architectures to validate the observed phenomena.
• The study suggests that strategies like adaptive batch sizing and data augmentation could mitigate the negative effects on model generalization.

Large-Batch Training for Deep Learning: Understanding the Generalization Gap

This paper investigates the effects of large-batch training on deep learning models, focusing on the observed generalization gap and the tendency of large-batch methods to converge to sharp minima. It explores the causes of these phenomena and proposes potential remedies. The main observation is that large-batch methods often lead to sharp minimizers, resulting in poorer generalization compared to small-batch methods, which naturally converge to flatter minimizers.

Introduction to the Problem

Deep learning has become foundational in large-scale machine learning, addressing diverse tasks such as computer vision and NLP. Training these models involves optimizing non-convex functions, typically approached with Stochastic Gradient Descent (SGD) and its variants. However, as batch sizes increase, there is a notable decrease in generalization performance despite similar training function values, attributed to convergence towards sharp minimizers. This generalization gap poses a challenge in leveraging large-batch training for improved parallelization in deep learning tasks.

Observations and Hypothesis

The core hypothesis proposed is the inclination of large-batch methods to converge to sharp minimizers with poorer generalization capabilities. A sharp minimizer is characterized by rapid variation in loss function values around the minima, resulting in a lack of generalization on unseen data. In contrast, small-batch methods, due to noise in gradient estimation, tend to find flat minimizers, which generalize better. This hypothesis is supported by both numerical experiments and theoretical insights.

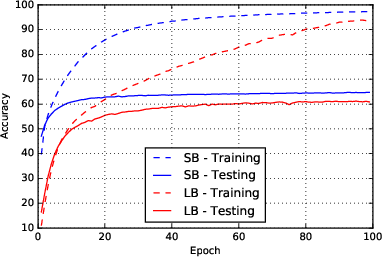
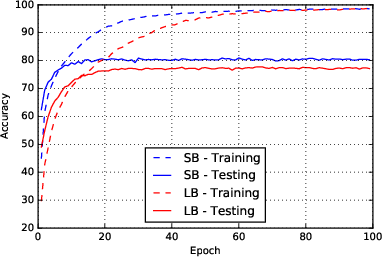
Figure 1: Network $F_2$

Experimental Evidence

The experiments involve training various neural network configurations using both small and large batch sizes, providing a comprehensive comparison of their respective generalization performances. Six network architectures were tested, and the data consistently supported the hypothesis. The training accuracy remained high across both methods; however, a significant discrepancy in testing accuracy was observed, corroborating the generalization gap experienced in large-batch scenarios.

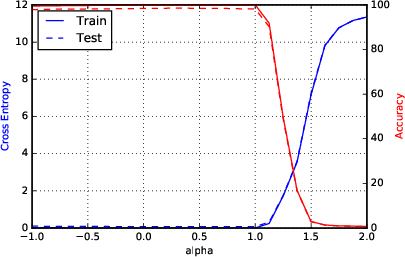
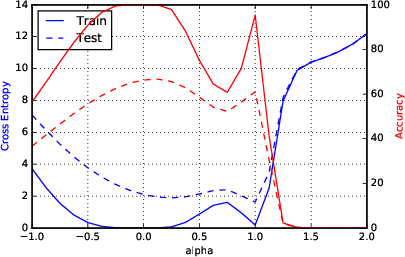
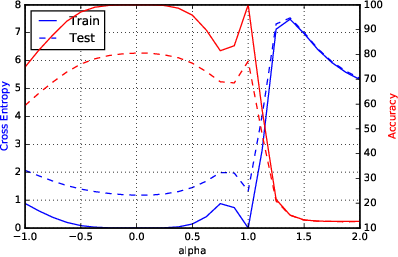
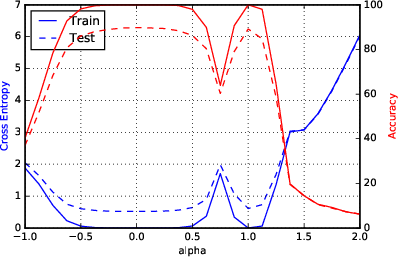
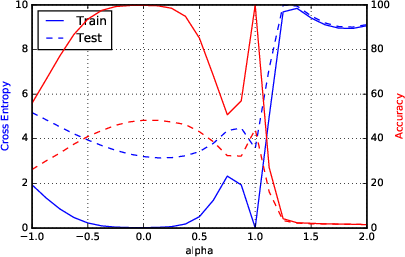
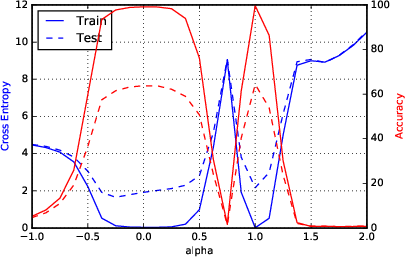
Figure 2: $F_1$ - Parametric Loss Curves Illustrating Sharp Minima for Large-Batch Methods.

Sharpness metrics were devised to quantitatively assess the nature of the minimizers. These metrics confirmed large-batch methods' convergence to sharp minimizers, highlighting increased sensitivity and explaining the observed generalization gap.

Remedies and Strategies

Efforts to mitigate the issues with large-batch training include data augmentation techniques and robust optimization. Data augmentation attempts to alter the geometry of the loss function, reducing its sensitivity, while robust optimization approaches aim to locate flatter minima by considering worst-case loss scenarios within a defined neighborhood.

Robust training, including adversarial approaches, did not significantly enhance generalization capabilities. Conservative training strategies, introducing proximal penalty terms to minimize sharpness, showed promise but failed to entirely resolve the challenges.

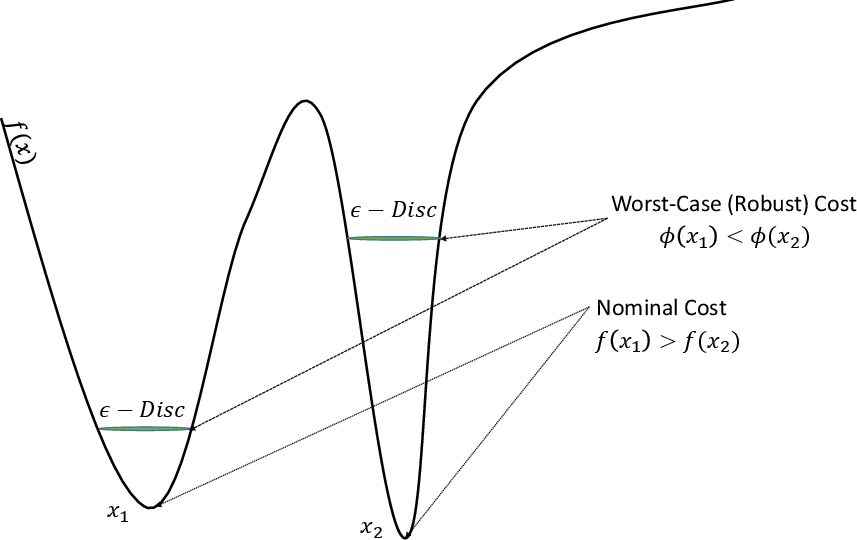
Figure 3: Illustration of Robust Optimization.

Success of Small-Batch Methods and Potential Solutions

Small-batch methods succeed due to their explorative properties, effectively escaping basins of sharp minimizers. Possible solutions for large-batch training might include adaptive batch sizing—a progressive increase during the training process—leveraging initial small-batch steps to steer away from sharp minima.

Conclusion

The investigation reveals crucial insights into the effects of large-batch training and the resultant generalization gap. While existing numerical observations and theoretical frameworks provide a foundation, further exploration into novel strategies and dynamic learning frameworks is essential for improving large-batch training methodologies. This paper stimulates future research into efficient large-batch optimizations and novel neural network architectures with enhanced compatibility for scalable deep learning tasks.