Scheduling Autonomous Vehicle Platoons Through an Unregulated Intersection (1609.04512v1)

Abstract: We study various versions of the problem of scheduling platoons of autonomous vehicles through an unregulated intersection, where an algorithm must schedule which platoons should wait so that others can go through, so as to minimize the maximum delay for any vehicle. We provide polynomial-time algorithms for constructing such schedules for a $k$-way merge intersection, for constant $k$, and for a crossing intersection involving two-way traffic. We also show that the more general problem of scheduling autonomous platoons through an intersection that includes both a $k$-way merge, for non-constant $k$, and a crossing of two-way traffic is NP-complete.

• The paper’s main contribution is a set of polynomial-time scheduling algorithms that minimize maximum delays for platoons at unregulated intersections.
• It employs parametric search and dynamic programming across various models, including one-way crossings, Y merges, and two-way intersections.
• The study also demonstrates NP-completeness in complex multiway merge scenarios, highlighting challenges in scaling autonomous traffic management.

Scheduling Autonomous Vehicle Platoons Through an Unregulated Intersection

Introduction

The problem of efficiently scheduling autonomous vehicle platoons through unregulated intersections is a significant challenge in the design of control algorithms for autonomous vehicle networks. The paper focuses on minimizing maximum delay for vehicles while ensuring traffic flows through unregulated intersections without collisions. Different intersection models including $k$-way merges and two-way crossings are analyzed for algorithmic solutions and computational complexity.

Definitions and Problem Setup

An intersection is modeled as a collection of incoming and outgoing lanes with constraints on simultaneous traffic flows. Platoons are defined by release times, lengths, and crossing times. The delay of a platoon is the difference between crossing time and release time, and the goal is to minimize the maximum delay within schedules. For simplicity, we prioritize scenarios such as one-way crossings, Y merges, and two-way crossings.

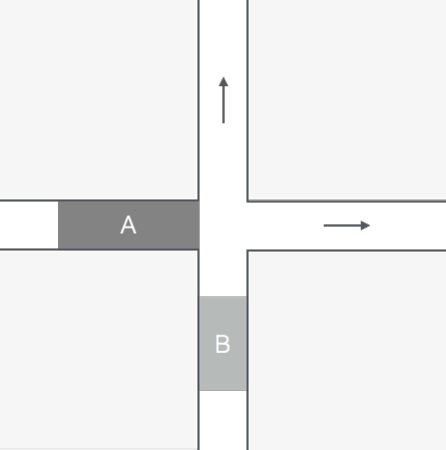
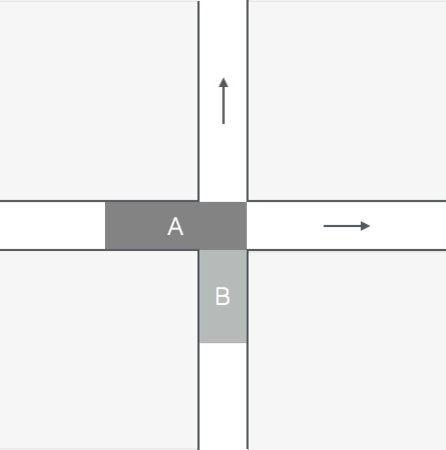
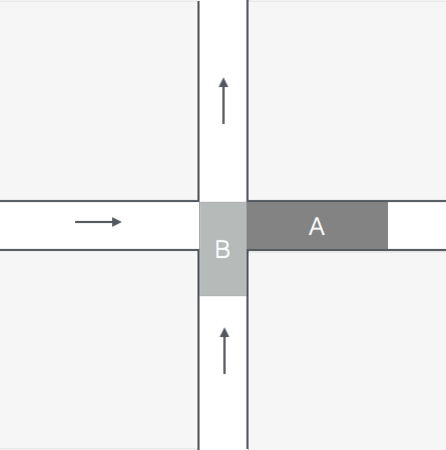
Figure 1: At t=0 platoon A, of length 3, reaches the intersection and begins to cross it. The release time of A is 0 and it's delay is also 0. Later at t=1 platoon B arrives at the intersection; its release time is 1 but it cannot cross immediately because A is in the intersection. Finally at t=3 B begins to cross, with delay 2. The delay of the overall schedule of these platoons is the maximum of the delays of the two platoons, 2.

Polynomial-time Algorithms

Parametric Search

The parametric search technique is employed to convert decision algorithms into optimization algorithms for finding minimum-delay schedules. This approach is used across different types of intersection models.

One-way Crossings and Y Merges

For one-way road crossings and Y merges, a greedy algorithm can be used to schedule platoons by prioritizing crossing based on arrival times. This ensures polynomial-time schedules with minimum delays.

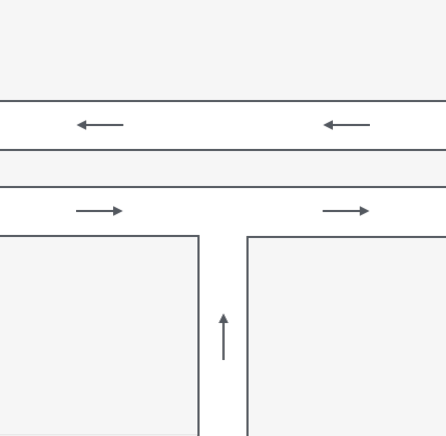
Figure 2: Three intersections that are mathematically equivalent in our model: (a) a crossing, (b) a Y merge, and (c) a T-junction.

Multiway Merges

Dynamic programming is used to handle $k$-way merges. This method examines possible states to determine the best sequence of platoon crossings that minimizes delays, achieving polynomial-time complexity depending on the number of lanes.

Two-way Crossings

Two-way crossings involve more complex scheduling due to bi-directional interference. A dynamic programming approach is applied similarly, considering states at times of switching between roads to maintain acceptable delays.

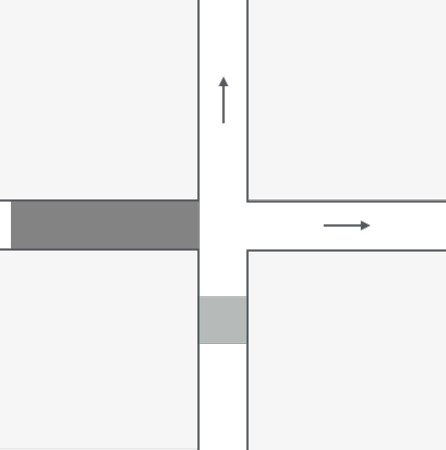
Figure 3: An example where crossing if possible is not always the best choice. Delaying the crossing of the long platoon, until the short platoon has cleared the intersection, reduces the maximum delay of the schedule.

Hardness of Scheduling Problems

The problem's complexity increases with non-constant $k$ in multiway merges and crossing scenarios. The paper proves that these problems become NP-complete when merging paths and cross traffic interfere in larger networks. The reduction from the PARTITION problem illustrates the challenge in scheduling without exceeding delays.

Figure 4: An example 5-way merge intersection.

Figure 5: A two-way crossing.

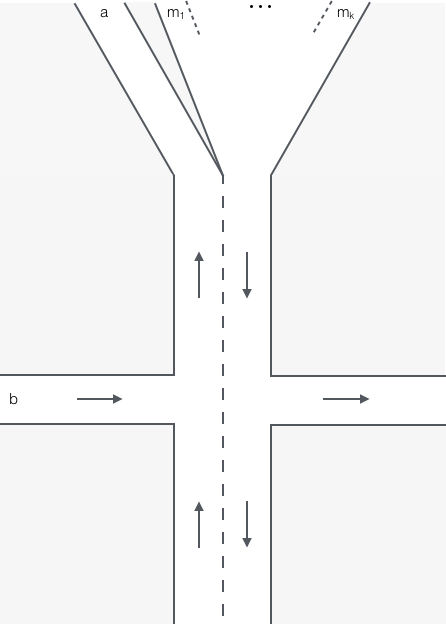
Figure 6: The intersection used in our hardness proof.

Conclusions

The paper provides polynomial-time solutions for specific intersection models and shows NP-completeness in more complex configurations. Future research may explore online scheduling where platoon paths are dynamic and unknown to further advance autonomous intersection management.