Layer Normalization (1607.06450v1)

Abstract: Training state-of-the-art, deep neural networks is computationally expensive. One way to reduce the training time is to normalize the activities of the neurons. A recently introduced technique called batch normalization uses the distribution of the summed input to a neuron over a mini-batch of training cases to compute a mean and variance which are then used to normalize the summed input to that neuron on each training case. This significantly reduces the training time in feed-forward neural networks. However, the effect of batch normalization is dependent on the mini-batch size and it is not obvious how to apply it to recurrent neural networks. In this paper, we transpose batch normalization into layer normalization by computing the mean and variance used for normalization from all of the summed inputs to the neurons in a layer on a single training case. Like batch normalization, we also give each neuron its own adaptive bias and gain which are applied after the normalization but before the non-linearity. Unlike batch normalization, layer normalization performs exactly the same computation at training and test times. It is also straightforward to apply to recurrent neural networks by computing the normalization statistics separately at each time step. Layer normalization is very effective at stabilizing the hidden state dynamics in recurrent networks. Empirically, we show that layer normalization can substantially reduce the training time compared with previously published techniques.

• The paper introduces layer normalization, a method that computes normalization statistics per layer rather than per mini-batch, enhancing training speed and stability.
• It demonstrates that by applying normalization at each layer and time step, recurrent neural networks achieve faster convergence and improved generalization.
• Experimental results show significant improvements in tasks like language modeling and question-answering, particularly in scenarios with small mini-batch sizes or variable sequence lengths.

Layer Normalization

Introduction and Background

Layer normalization is introduced as a method to improve the training speed and stability of deep neural networks. The primary motivation behind this research is the computational cost associated with training neural networks and the limitations of previous normalization techniques, such as batch normalization, particularly in recurrent neural networks (RNNs). Layer normalization provides a way to normalize summed inputs to neurons based on layer-wise statistics instead of batch-wise statistics to enhance trainability and diminish dependence on mini-batch sizes.

Batch normalization standardizes inputs over mini-batches, which can be problematic for RNNs due to varying sequence lengths and the necessity to maintain statistics for different time steps. This paper addresses these limitations by proposing layer normalization, which normalizes across the inputs to a layer within a single training instance, allowing it to be effective in various settings, including RNNs.

Methodology

Layer normalization fundamentally changes how normalization is applied within neural networks. For a given hidden layer in a neural network, layer normalization computes normalization statistics, specifically the mean and variance, over all summed inputs to neurons within that layer, rather than across a mini-batch. Hence, all neurons in a layer share the same normalization terms, but different training samples have their unique normalization parameters. The proposed method can naturally extend to RNNs by applying it at each time step independently, thereby stabilizing hidden state dynamics.

The efficacy of layer normalization is in its ability to produce consistent normalization at training and test times without the need for mini-batch statistics. This is critical in settings where batch normalization fails, such as in small mini-batches or online learning tasks.

Experimental Results

Layer normalization demonstrated significant improvements across several experimental tasks, particularly those involving RNNs. It showed reduced training times and better generalization over baseline models in tasks including image-sentence ranking, question-answering, language modeling, generative modeling, and MNIST classification.

• Image-Sentence Ranking: Layer normalization sped up the convergence and improved retrieval performance (Figure 1).

(Figure 1)

Figure 1: Recall@K curves using order-embeddings with and without layer normalization.

• Question-Answering: Layer normalization improved validation accuracy and convergence rates in attentive reader models compared to batch normalization alternatives.
• Language Modeling: In skip-thoughts models, it resulted in faster training convergence and superior performance on downstream tasks.
• Generative Modeling: On tasks like handwriting sequence generation, layer normalization provided increased convergence speed, particularly beneficial for long sequences and models trained with small mini-batches (Figure 2).

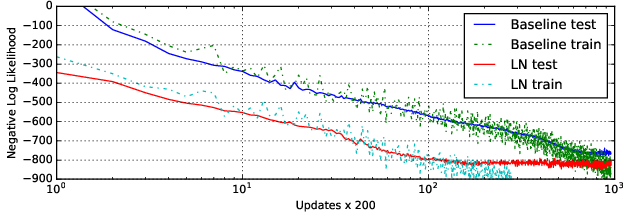
  Figure 2: Handwriting sequence generation model negative log likelihood with and without layer normalization.

• MNIST Classification: While it performed robustly across varying batch sizes compared to batch normalization, its applicability to convolutional neural networks (ConvNets) was not as pronounced due to differing distributional assumptions of hidden unit activations (Figure 3).

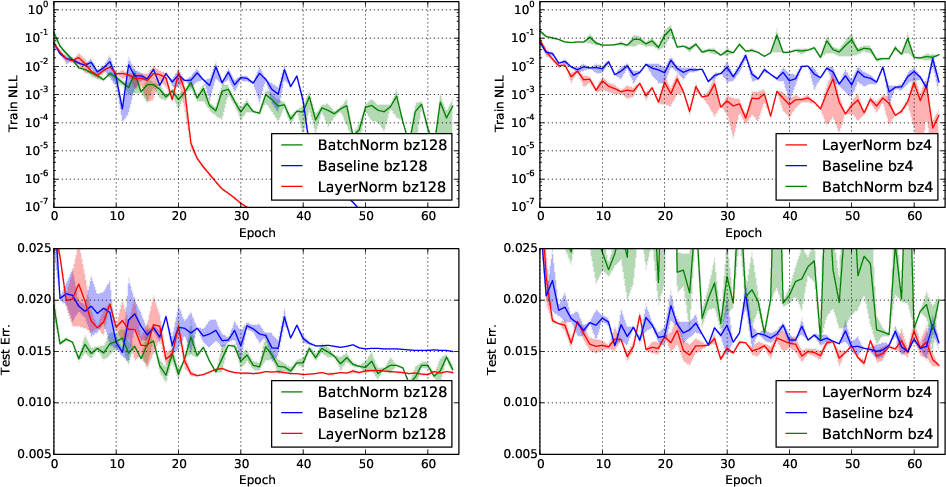
  Figure 3: Permutation invariant MNIST model negative log likelihood and test error with layer and batch normalization.

Invariance and Geometry Analysis

Layer normalization is distinct in its invariance properties under data and weight transformations compared to other normalization techniques. It remains invariant to per-training case feature shifting and scaling, simplifying the learning dynamics and potentially stabilizing training. Additionally, the Fisher information matrix analysis in parameter space suggests that layer normalization can offer implicit learning rate reduction, stabilizing training without necessitating manual learning rate scheduling.

Conclusion

Layer normalization emerges as a versatile, efficient normalization technique crucial for the rapid and stable training of neural networks, particularly those with recurrence or employed in online settings. It overcomes the constraints of batch normalization and improves learning dynamics without entailing additional dependencies. The continuation of this work could involve optimizing performance within convolutional architectures and exploring further applications across diverse AI models.