Efficient Representation of Low-Dimensional Manifolds using Deep Networks (1602.04723v1)

Abstract: We consider the ability of deep neural networks to represent data that lies near a low-dimensional manifold in a high-dimensional space. We show that deep networks can efficiently extract the intrinsic, low-dimensional coordinates of such data. We first show that the first two layers of a deep network can exactly embed points lying on a monotonic chain, a special type of piecewise linear manifold, mapping them to a low-dimensional Euclidean space. Remarkably, the network can do this using an almost optimal number of parameters. We also show that this network projects nearby points onto the manifold and then embeds them with little error. We then extend these results to more general manifolds.

• The paper introduces a network architecture that efficiently embeds monotonic chains representing low-dimensional manifolds with near-optimal parameter use.
• It details the method’s theoretical guarantees, including continuity of embeddings and error bounds in the presence of noise.
• Empirical results on the Swiss Roll and face images validate the approach for dimensionality reduction and manifold learning.

Efficient Representation of Low-Dimensional Manifolds Using Deep Networks

Introduction

The paper explores the capabilities of deep neural networks in representing data located near low-dimensional manifolds within high-dimensional spaces. The authors demonstrate that these networks can efficiently derive intrinsic coordinates of such data. Specifically, deep networks' initial layers can embed points residing on monotonic chains, which are special types of piecewise linear manifolds, into low-dimensional Euclidean spaces using an almost optimal number of parameters.

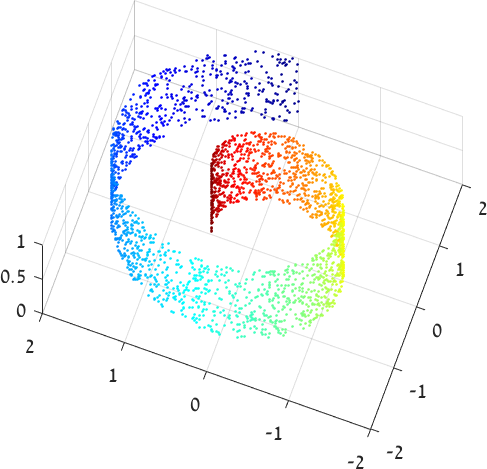
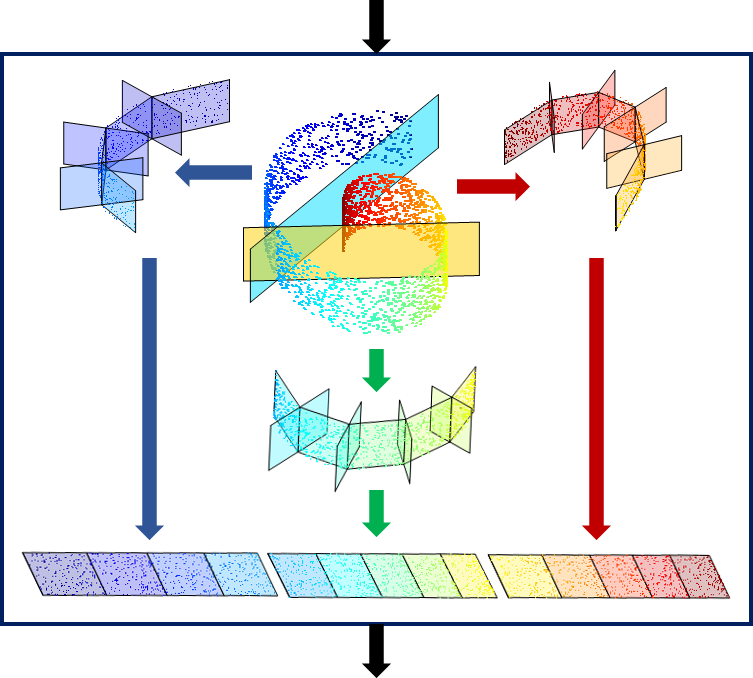
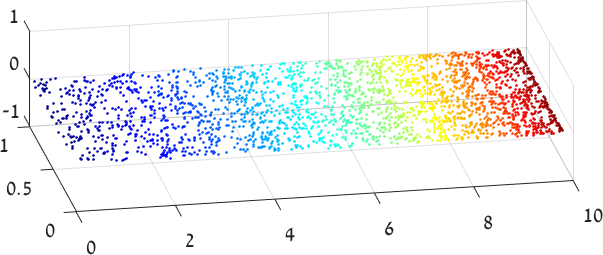
Figure 1: We illustrate the embedding of a manifold by a deep network using the famous Swiss Roll example (top). Dots represent color coded input data. In the center, the data is divided into three parts using hidden units represented by the yellow and cyan planes. Each part is then approximated by a monotonic chain of linear segments. Additional hidden units, also depicted as planes, control the orientation of the next segments in the chain. A second layer of the network then flattens each chain into a 2D Euclidean plane, and assembles these into a common 2D representation (bottom).

Monotonic Chains and Network Construction

The authors detail a network architecture utilizing two layers capable of precisely embedding monotonic chains—linked linear segments. These networks are constructed to efficiently map manifold structures represented by these chains into lower-dimensional spaces.

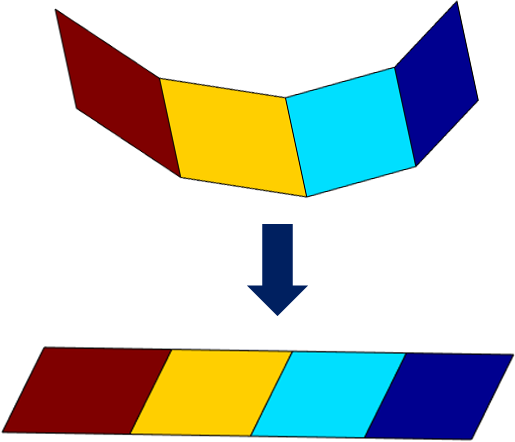
Figure 2: A continuous chain of linear segments (above) that can be flattened to lie in a single low-dimensional linear subspace (bottom).

Initializing the network involves associating each segment of a monotonic chain with specific hidden units, encoding both the chain's structure and allowing for efficient parameter use across the network layers. The paper provides theoretical proofs of the embedding's continuity for adjacent segments using a series of mathematical constructs.

Error Analysis

The paper acknowledges potential errors when points slightly deviate from the monotonic chain due to noise or non-linear approximations. It provides a worst-case error scenario analysis, illustrating cases where errors can increase significantly based on chain configurations and hyperplane separations.

In practical settings, when hyperplanes adequately separate the segments, error bounds remain modest, thus ensuring the network's reliability in embedding even slightly perturbed points.

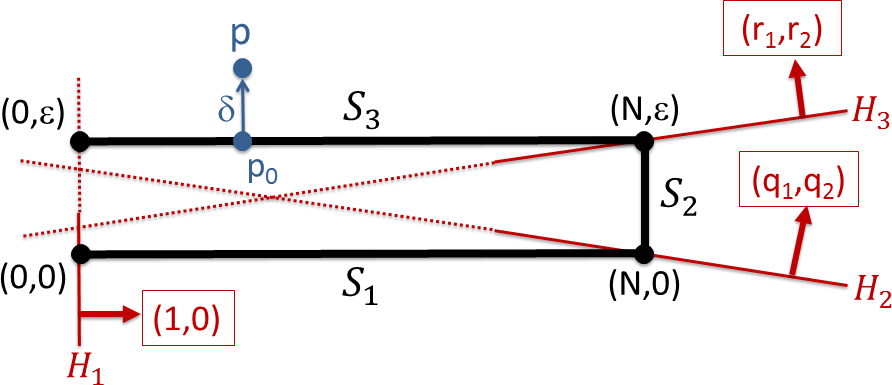
Figure 3: In black, we show a 1D monotonic chain with three segments. In red, we show three hidden units that flatten this chain into a line. Note that each hidden unit corresponds to a hyperplane (in this case, a line) that separates the segments into two connected components. The third hyperplane must be almost parallel to the third segment. This leads to large errors for noisy points near $S_3$.

Experiments

The authors implement practical examples showcasing the constructed networks' performance, such as the Swiss Roll example and a set of face images represented as manifolds. These examples visually affirm the network's ability to efficiently represent complex, low-dimensional manifolds across varying data sets.

Figure 4: The output of a network that approximates images of a face using a monotonic chain. Each dot represents an image. They are coded by size to indicate elevation, and color to indicate azimuth. At four dots, we display the corresponding face images.

Implications and Future Work

This research suggests that deep networks might be employed effectively for dimensionality reduction with substantial efficiency. Their ability to add linear segments with few additional parameters highlights potential directions for optimizing neural architectures dedicated to manifold learning.

Moreover, it indicates a larger narrative regarding the inherent constraints deep networks face despite their extensive power in creating piecewise linear regions. Understanding the roles of individual units in shaping learned functions opens pathways for future explorations in neural system designs and potential applications.

Conclusion

The paper provides a comprehensive analysis supporting the utility of deep networks in modeling low-dimensional manifolds efficiently within high-dimensional spaces. It details the network architectures, parameter efficiency, and potential real-world application scenarios such networks could address. The implications suggest promising future explorations in the neural network domain, especially in optimizing architectures used for manifold-based data representations.