Sliced Wasserstein Kernels for Probability Distributions (1511.03198v1)

Published 10 Nov 2015 in cs.LG and stat.ML

Abstract: Optimal transport distances, otherwise known as Wasserstein distances, have recently drawn ample attention in computer vision and machine learning as a powerful discrepancy measure for probability distributions. The recent developments on alternative formulations of the optimal transport have allowed for faster solutions to the problem and has revamped its practical applications in machine learning. In this paper, we exploit the widely used kernel methods and provide a family of provably positive definite kernels based on the Sliced Wasserstein distance and demonstrate the benefits of these kernels in a variety of learning tasks. Our work provides a new perspective on the application of optimal transport flavored distances through kernel methods in machine learning tasks.

Citations (154)

View on Semantic Scholar

Summary

The paper introduces novel Sliced Wasserstein Kernels that use one-dimensional projections for efficient computation of optimal transport distances.
It rigorously proves the positive definiteness of the proposed kernels, enabling effective application in SVMs, kernel PCA, and clustering tasks.
Experimental results on texture and animal face datasets demonstrate significant improvements in data variance capture, accuracy, and clustering quality.

Sliced Wasserstein Kernels for Probability Distributions

Introduction

"Sliced Wasserstein Kernels for Probability Distributions" explores a novel approach to leveraging optimal transport distances, specifically the Sliced Wasserstein distance, within the context of kernel methods in machine learning and computer vision tasks. The paper aims to integrate the advantages of waveform transport metrics with the flexibility and theoretical foundation of kernel methods, resulting in a family of kernels that are both theoretically robust and practically efficient.

Background

Optimal transport distances, notably the Wasserstein distance, offer a robust framework for quantifying discrepancies between probability distributions. This utility is especially pronounced in applications involving histogram-based methods, feature matching, and visualization of image intensity variations. Despite these strengths, computational burdens associated with calculating these distances, particularly in higher dimensions, have historically limited their application.

The Sliced Wasserstein distance is applied wherein a given high-dimensional distribution is reduced to multiple one-dimensional representations via projections. These projections facilitate the computation of Wasserstein distances in a computationally efficient manner due to the availability of closed-form solutions for one-dimensional cases.

Positive Definite Kernels and Kernel Methods

The paper provides a rigorous mathematical foundation proving that the Sliced Wasserstein distance meets the criteria for constructing positive definite kernels, which can be used in kernel methods such as SVMs, kernel PCA, and kernel $k$ -means clustering. Establishing the positive definiteness is crucial since it ensures the method's validity for a wide range of applications, allowing it to leverage typical kernel trick conveniences for efficient computation and embedding in high-dimensional spaces.

Sliced Wasserstein Kernels

Two forms of Sliced Wasserstein kernels are introduced: the Gaussian and polynomial kernels. These kernels are provably positive definite on the space of probability distributions. An innovative feature of this system is the explicit invertible mapping to the kernel space, a step that greatly facilitates downstream tasks, making these kernels adaptable to various learning paradigms.

Experimental Results

Experiments were conducted on the UIUC texture and LHI animal face datasets, showcasing the efficacy of the Sliced Wasserstein kernels over traditional kernels like RBF and polynomial kernels.

Figure 1: The UIUC texture dataset with 25 classes (a), the corresponding calculated co-occurrence matrices (b), and the kernel representation (i.e. $\phi_\sigma$ ) of the co-occurrence matrices (c).

Figure 2: The LHI animal face dataset with 21 classes (a), the corresponding calculated HOGgles representation (b), and the kernel representation (i.e. $\phi_\sigma$ ) of the HOGgles images (c).

Critical observations include the superior capturing of dataset variance using Sliced Wasserstein kernel PCA as well as improvements in classification accuracy and clustering quality, as evidenced by metrics such as CPV and V-measure.

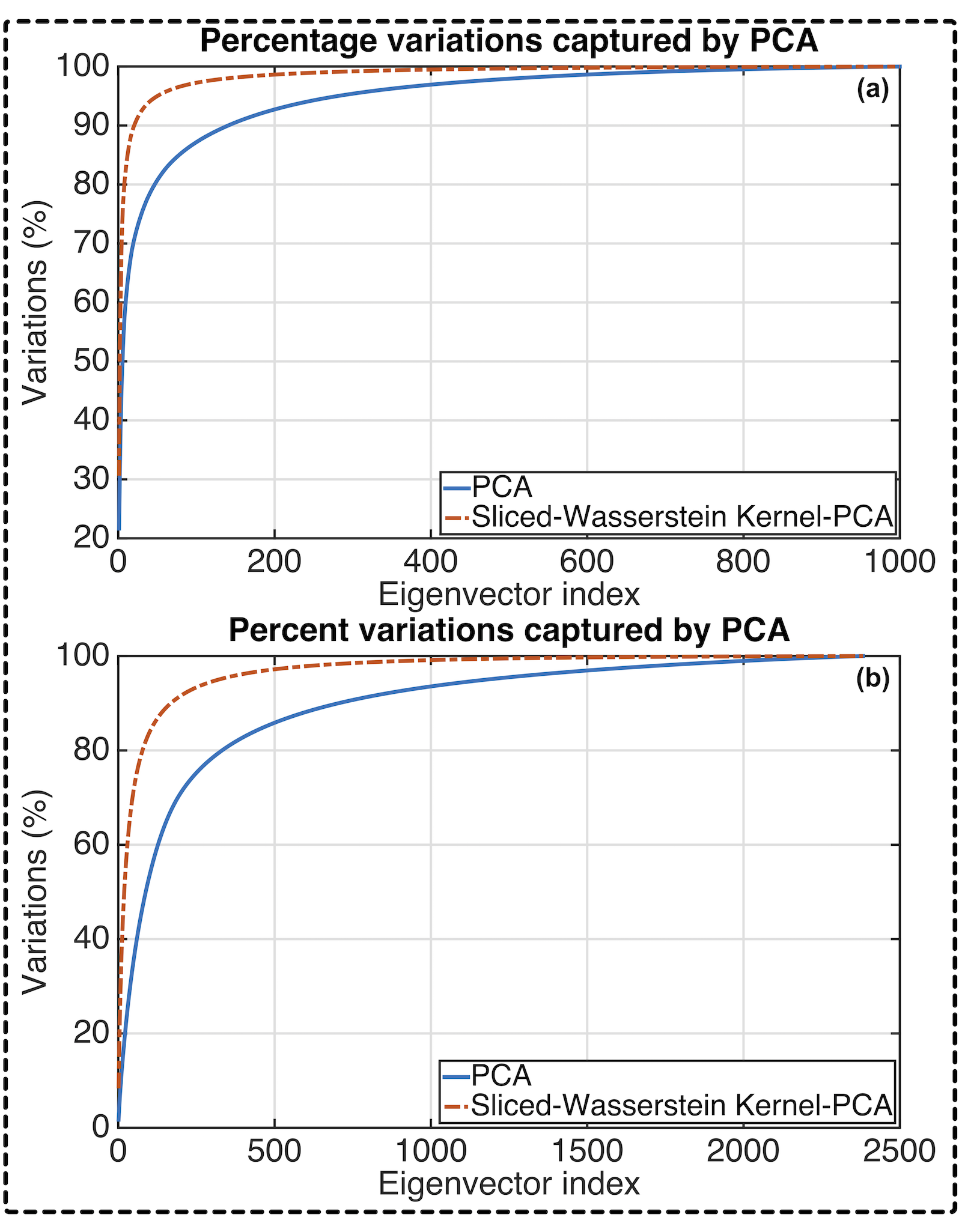
Figure 3: Percentage variations captured by eigenvectors calculated from PCA and calculated from Sliced Wasserstein kernel PCA for the texture dataset (a) and for the animal face dataset (b).

Discussion and Future Directions

The demonstrated improvements in capturing data variance and achieve higher classification accuracy reinforce the potential of Sliced Wasserstein kernels as a powerful tool in processing probability distributions. The methodological framework serves as a stepping stone for exploring applications beyond two-dimensional datasets into volumetric and higher-dimensional data spaces such as MRI/CT data.

The paper opens avenues for deeper investigation into complex data modalities, and future work will likely explore enhanced scalability and integration with other machine learning architectures, potentially incorporating neural network frameworks that cater to probability distribution data. The versatility and efficiency of these kernels forecast significant contributions to advancing state-of-the-art techniques in pattern recognition and image analysis.

Conclusion

The integration of optimal transport distances with kernel methods through the Sliced Wasserstein distance introduces a promising new direction in machine learning. The paper has successfully established the groundwork for applying these concepts to improve pattern recognition tasks, with implications that extend across various domains requiring robust distributional comparison measures. Further research and application will continue to expand the utility and impact of these methods in practical and theoretical contexts alike.