Layer-Specific Adaptive Learning Rates for Deep Networks (1510.04609v1)

Abstract: The increasing complexity of deep learning architectures is resulting in training time requiring weeks or even months. This slow training is due in part to vanishing gradients, in which the gradients used by back-propagation are extremely large for weights connecting deep layers (layers near the output layer), and extremely small for shallow layers (near the input layer); this results in slow learning in the shallow layers. Additionally, it has also been shown that in highly non-convex problems, such as deep neural networks, there is a proliferation of high-error low curvature saddle points, which slows down learning dramatically. In this paper, we attempt to overcome the two above problems by proposing an optimization method for training deep neural networks which uses learning rates which are both specific to each layer in the network and adaptive to the curvature of the function, increasing the learning rate at low curvature points. This enables us to speed up learning in the shallow layers of the network and quickly escape high-error low curvature saddle points. We test our method on standard image classification datasets such as MNIST, CIFAR10 and ImageNet, and demonstrate that our method increases accuracy as well as reduces the required training time over standard algorithms.

• The paper introduces a method that computes layer-specific learning rates based on gradient magnitudes to mitigate vanishing gradients and saddle point issues.
• The proposed technique dynamically adjusts rates across network layers, reducing training time by about 15% on large datasets like ImageNet.
• Experimental evaluations on MNIST, CIFAR10, and ImageNet demonstrate improved convergence, enhanced accuracy, and lower loss compared to traditional SGD methods.

Layer-Specific Adaptive Learning Rates for Deep Networks

Introduction

The advancement of deep neural networks has resulted in remarkable performance in several domains, including image classification, face recognition, sentiment analysis, and speech recognition. However, with the increase in complexity of these architectures, training time has substantially grown, often extending to weeks or months due to the "vanishing gradients" and the proliferation of high-error low-curvature saddle points. The paper proposes a method wherein learning rates are both layer-specific and adaptive, tailored to overcome these obstacles by accelerating learning in shallow layers and efficiently escaping saddle points.

Gradient Descent Techniques

Stochastic Gradient Descent (SGD) has long been a staple for optimizing deep networks despite its sensitivity to learning rate choices. It updates weights iteratively based on approximate gradients and adjusts the learning rate according to a pre-defined decay rule. In contrast, methods like Newton's method and AdaGrad offer alternative approaches to optimization, each with unique strategies for handling gradients and learning rates. AdaGrad, notably, adjusts the learning rate relative to the history of gradients, while struggling with diminishing rates over extensive iterations.

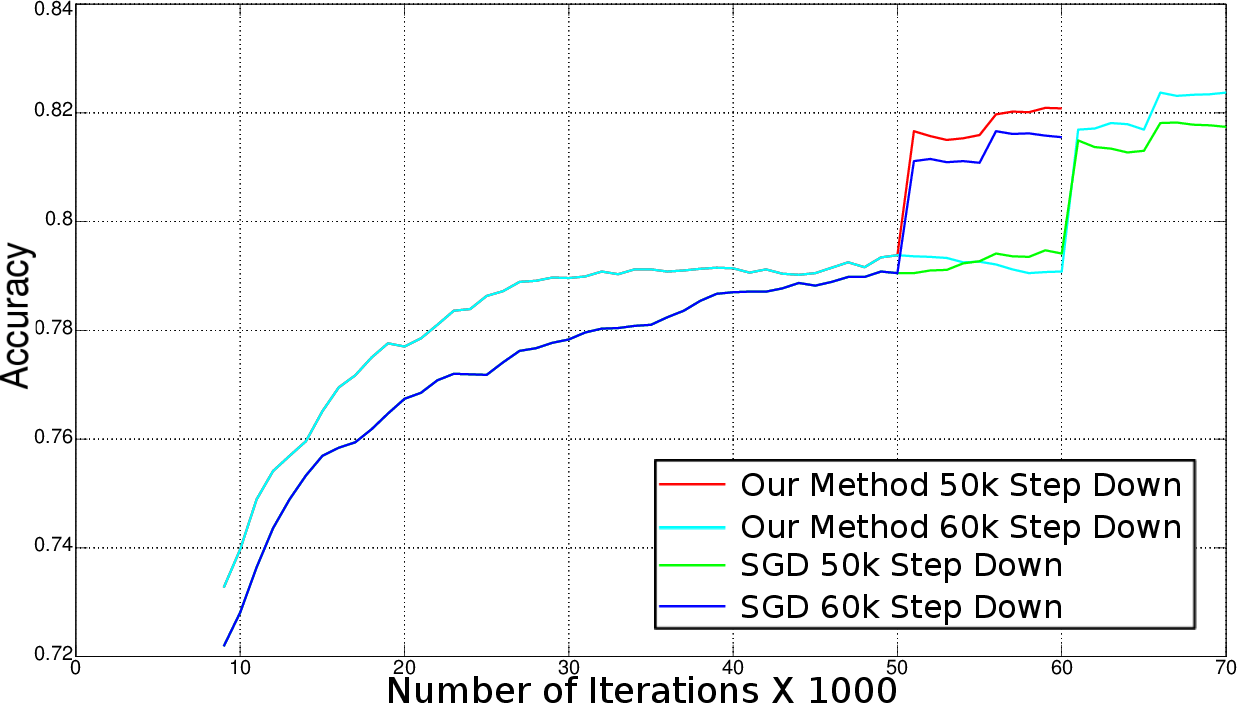
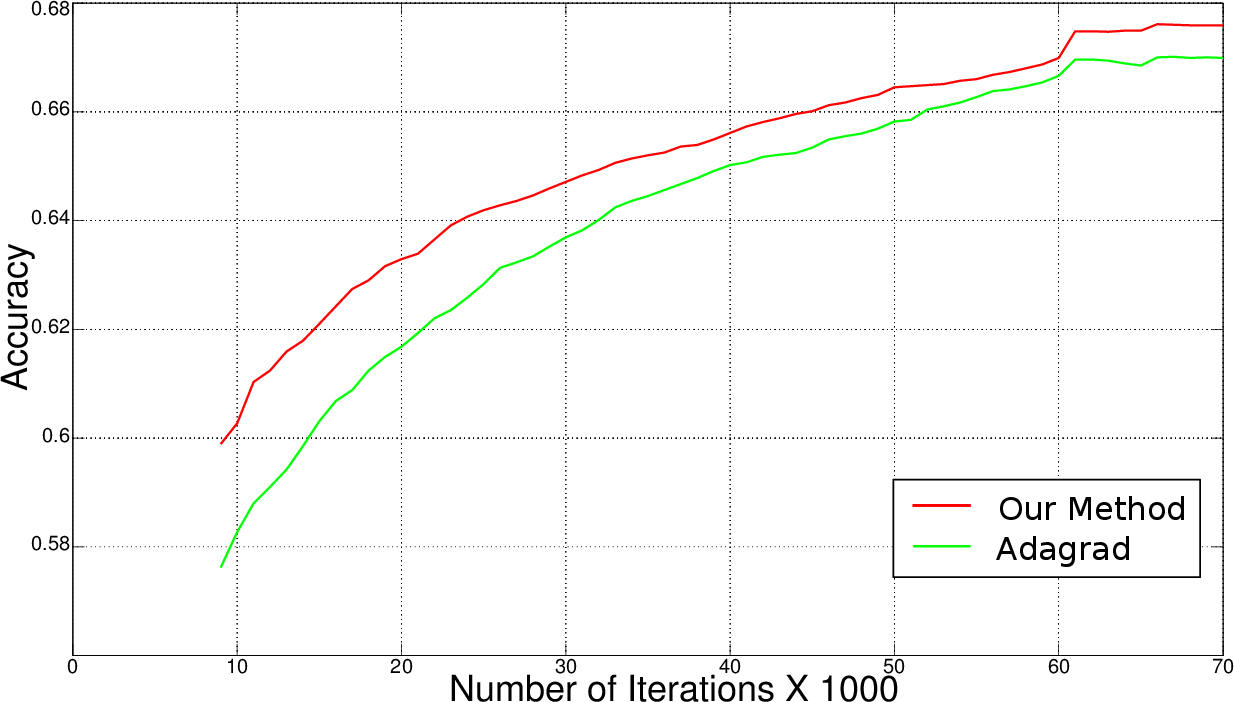
Figure 1: Stochastic Gradient Descent.

Proposed Method

The core innovation of the proposed methodology is layer-specific learning rates adjusted relative to the gradient magnitude specific to each layer. This approach counteracts the slow learning endemic to shallower network layers by allowing faster training through increased learning rates at lower curvature points. The calculation of learning rates via the formula $$t^{(k)}_l = t^{(k)} (1 + \log (1+ 1/(\| g^{(k)}_l \|_2)))$$ ensures efficient learning by scaling learning rates appropriately.

This methodology is applicable to a range of traditional gradient techniques, facilitating improved convergence and computational efficiency without extensive memory requirements, as gradients from previous iterations are not stored. By increasing learning rates at saddle points, the method ensures robust convergence even in high-dimensional non-convex spaces.

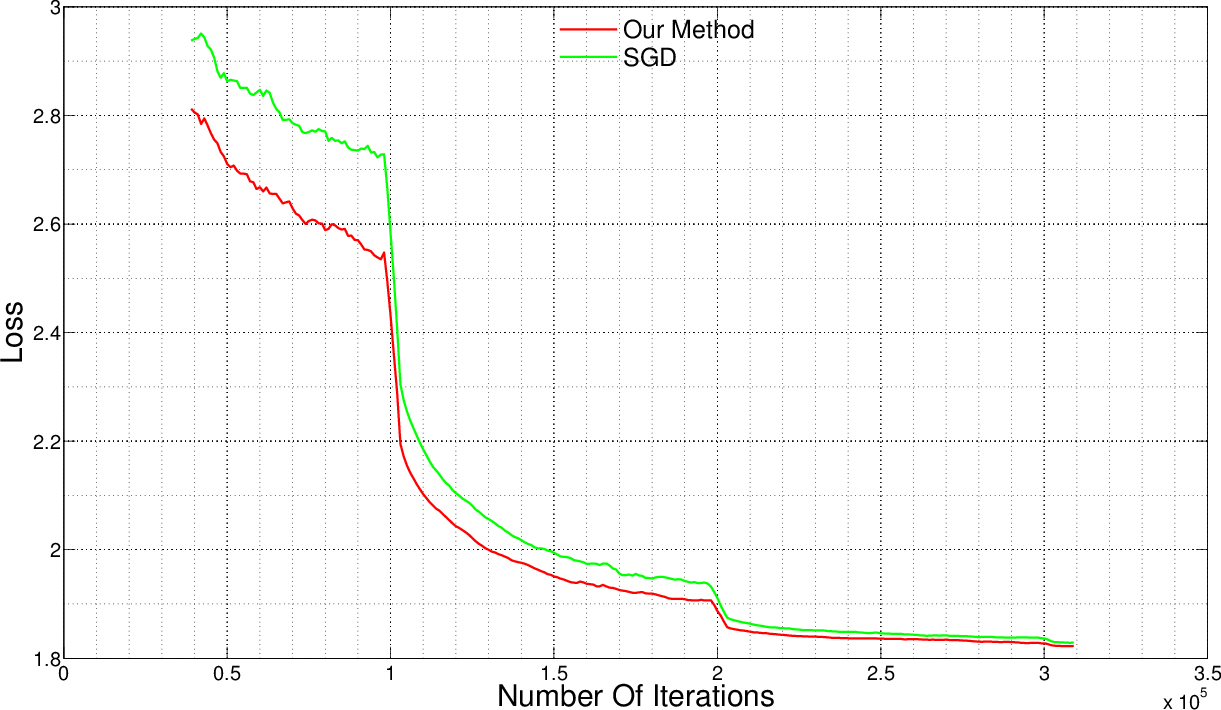
Figure 2: Loss with Stochastic Gradient Descent.

Experimental Results

Testing on standard datasets such as MNIST, CIFAR10, and ImageNet demonstrated notable improvements in accuracy and reduction in training time. On MNIST, layer-specific adaptive learning rates consistently improved performance compared to other methods across iterations. CIFAR10 and ImageNet tests revealed the method’s capability to achieve higher accuracy and lower loss in fewer iterations compared to traditional methods. For instance, the proposed method shortened training time by approximately 15% on ImageNet, a significant achievement given the scale of the dataset.

Conclusions

The introduction of layer-specific adaptive learning rates represents a significant step forward in optimizing the training of deep neural networks. By addressing the inherent challenges of vanishing gradients and saddle points, this method offers both practical and theoretical benefits, enabling more efficient training processes with minimal computational cost increases. Future developments could explore further refinements and applications across various architectures and datasets, potentially enhancing the robustness and applicability of deep learning systems.

In summary, the paper presents a viable solution for improving deep network training by leveraging intrinsic layer characteristics to tailor learning rates, thus facilitating faster convergence and enhanced model performance across diverse datasets and complex architectures.