Finite Volume Modeling of Poroelastic-Fluid Wave Propagation with Mapped Grids (1305.2952v1)

Abstract: In this work we develop a high-resolution mapped-grid finite volume method code to model wave propagation in two dimensions in systems of multiple orthotropic poroelastic media and/or fluids, with curved interfaces between different media. We use a unified formulation to simplify modeling of the various interface conditions -- open pores, imperfect hydraulic contact, or sealed pores -- that may exist between such media. Our numerical code is based on the Clawpack framework, but in order to obtain correct results at a material interface we use a modified transverse Riemann solution scheme, and at such interfaces are forced to drop the second-order correction term typical of high-resolution finite volume methods. We verify our code against analytical solutions for reflection and transmission of waves at a material interface, and for scattering of an acoustic wave train around an isotropic poroelastic cylinder. For reflection and transmission at a flat interface, we achieve second-order convergence in the 1-norm, and first-order in the max-norm; for the cylindrical scatterer, the highly distorted grid mapping degrades performance but we still achieve convergence at a reduced rate. We also simulate an acoustic pulse striking a simplified model of a human femur bone, as an example of the capabilities of the code. To aid in reproducibility, at the web site http://dx.doi.org/10.6084/m9.figshare.701483 we provide all of the code used to generate the results here.

• The paper develops a high-resolution finite volume method to simulate wave propagation in poroelastic and fluid media using mapped grids.
• It implements modified flux approaches to accurately handle complex interface conditions and anisotropic behaviors at material boundaries.
• Numerical results demonstrate consistent second-order convergence and practical accuracy in simulating plane waves and resonance-like behaviors.

Finite Volume Modeling of Poroelastic-Fluid Wave Propagation with Mapped Grids

Introduction

The paper introduces a high-resolution finite volume method designed to model wave propagation in systems containing multiple poroelastic media and/or fluids. This method is implemented using mapped grids to accommodate curved interfaces between distinct materials. This section focuses on the underlying framework and highlights the importance of poroelastic theory, introduced by Maurice A. Biot, which extends the mechanics of fluid-saturated porous media through homogenization techniques. Applications extend to in vivo bone modeling and underwater acoustics.

Governing Equations and Interface Conditions

Poroelastic media require a first-order linear system of PDEs, where anisotropic properties translate to orthotropic behavior—a setup where deformation across different material axes is independent. The paper discusses handling media composed of fluid and poroelastic materials, utilizing Biot’s equality of energy partition within propagating waves. Interface conditions play a crucial role, handled via Deresiewicz and Skalak's imperfect hydraulic contact condition. Between poroelastic media, interface conditions are related to pressure differentials and fluid flow continuity.

Mapped Grid Finite Volume Methods

Mapped grids offer advantages over unstructured grids due to reduced computational overhead and simpler data structures. However, implementing finite volume methods for anisotropic media creates challenges when dealing with arbitrary grid orientations. The paper discusses modifications required for the classical high-resolution finite volume method, particularly at interfaces where poroelastic material meets a fluid. Traditional methods may inaccurately transmit poroelastic stress and velocities into fluid regions, necessitating a revised flux approach.

Figure 1: Example of a mapped grid, showing computational space at the left and physical space at the right.

Riemann Problem Solutions

The solution of Riemann problems is vital for high-resolution finite volume methods. The paper simplifies the eigenproblem from an 8x8 unsymmetric matrix to a 4x4 symmetric-definite form by utilizing properties of poroelastic and acoustic systems. Further reduction employs factorization and orthonormalization techniques to effectively find eigenvectors corresponding to wave families in different media.

Numerical Results

Simulation results demonstrate the efficacy of the method in handling rectilinear grids and interfaces. Noteworthy is the omission of the second-order correction term, which traditionally improves accuracy but presents challenges at material interfaces. The paper reports consistent second-order convergence for various test cases, highlighting the solution’s applicability in modeling plane waves reflected and transmitted at interfaces.

Figure 2: Variation of the condition number of the Riemann solution linear system.

Mapped Grid Scenarios

Attention is given to cylindrical scatterer scenarios with complex grid mappings crucial for modeling resonance-like behavior at specific frequencies. Despite reduced convergence rates due to grid distortions, the paper underscores the practical accuracy achieved across fine grid simulations. Suggestions for future work involve adaptive mesh refinement and potential transitions to three-dimensional modeling.

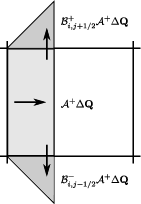
Figure 3: Comparison of classical and fluctuation-based approaches to cell updates from transverse Riemann solves.

Conclusion

The paper effectively extends previous work on finite volume modeling to incorporate mapped grids, addressing challenges such as non-rectilinear interfaces and varied hydraulic conditions. It posits future enhancements in second-order corrections and three-dimensional modeling capabilities, alongside potential improvements in the accuracy of stiff regime solutions through advanced eigenvector solutions or exponential time-integrators.

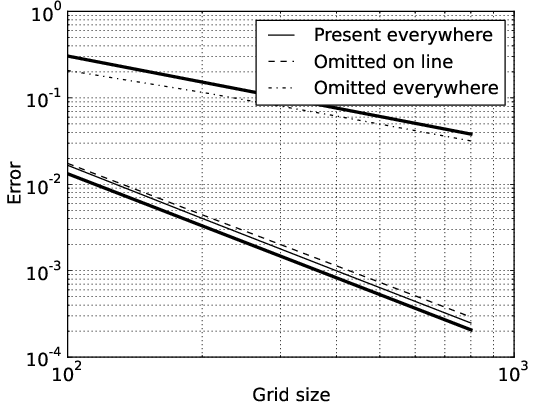
Figure 4: Detailed examination of the effect of omitting the second-order correction term for the case with lowest convergence rate.